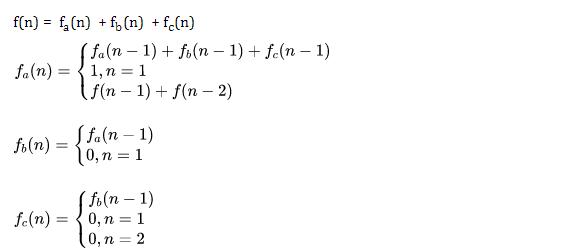定义问题的递归函,明确函数的功能,我们定义这个函数的功能为:把A上面的n个圆盘经由B移到C
// 将 n 个圆盘从 a 经由 b 移动到 c 上 public void hanoid(int n, char a, char b, char c) { }查找问题与子问题的关系 首先我们看如果A柱子上只有两块圆盘该怎么移
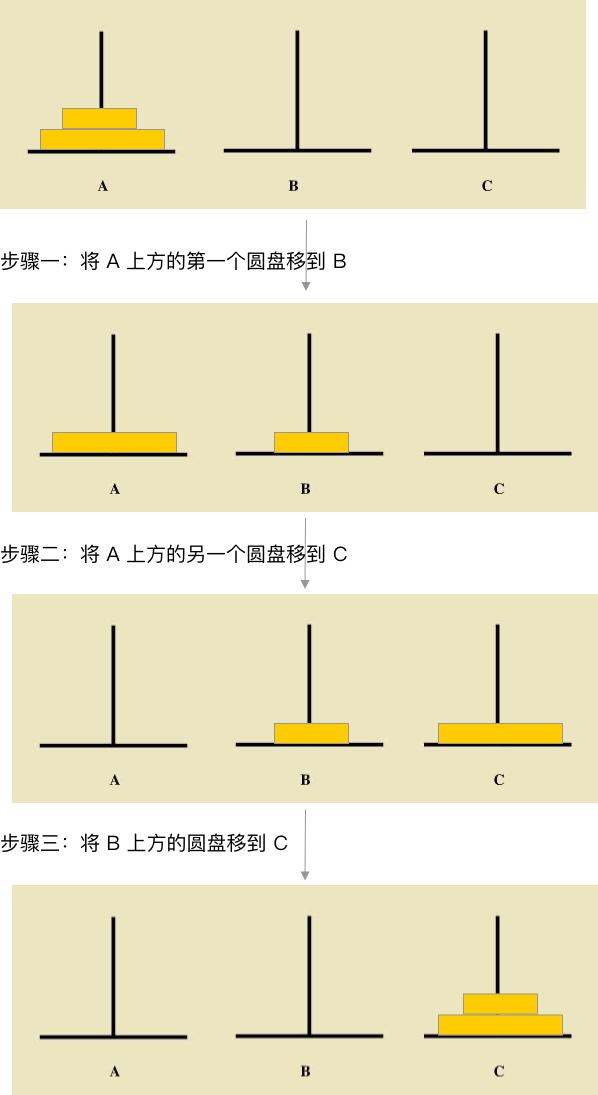
前面我们多次提到,分析问题与子问题的关系要采用自上而下的分析方式,要将n个圆盘经由B移到C柱上去,可以按以下三步来分析
a. 将上面的n-1个圆盘看成是一个圆盘,这样分析思路就与上面提到的只有两块圆盘的思路一致了
b. 将上面的n-1个圆盘经由C移到B,此时将 A 底下的那块最大的圆盘移到C
c. 再将B上的n-1个圆盘经由A移到C上
有人问第一步的n-1怎么从C移到B,重复上面的过程,只要把上面的n-2个盘子经由A移到B,再把A最下面的盘子移到C,最后再把上面的n-2的盘子经由A移到B下..., 怎么样,是不是找到规律了,不过在找问题的过程中切忌把子问题层层展开,到汉诺塔这个问题上切忌再分析n-3,n-4 怎么移,这样会把你绕晕,只要找到一层问题与子问题的关系得出可以用递归表示即可。
由以上分析可得
move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C`)一定要先得出递归公式,哪怕是伪代码也好!这样第三步推导函数编写就容易很多,终止条件我们很容易看出,当 A上面的圆盘没有了就不移了
根据以上的递归伪代码补充函数的功能
// 将 n 个圆盘从 a 经由 b 移动到 c 上 public void hanoid(int n, char a, char b, char c) { if (n <= 0) { return; } // 将上面的 n-1 个圆盘经由 C 移到 B hanoid(n-1, a, c, b); // 此时将 A 底下的那块最大的圆盘移到 C move(a, c); // 再将 B 上的 n-1 个圆盘经由A移到 C上 hanoid(n-1, b, a, c); } public void move(char a, char b) { printf("%c->%c\n", a, b); }从函数的功能上看其实比较容易理解,整个函数定义的功能就是把 A 上的 n 个圆盘 经由 B 移到 C,由于定义好了这个函数的功能,那么接下来的把 n-1 个圆盘 经由 C 移到 B 就可以很自然的调用这个函数,所以明确函数的功能非常重要,按着函数的功能来解释,递归问题其实很好解析,切忌在每一个子问题上层层展开死抠,这样这就陷入了递归的陷阱,计算机都会栈溢出,何况人脑
时间复杂度分析 从第三步补充好的函数中我们可以推断出
f(n) = f(n-1) + 1 + f(n-1) = 2f(n-1) + 1 = 2(2f(n-2) + 1) + 1 = 2 * 2 * f(n-2) + 2 + 1 = 22 * f(n-3) + 2 + 1 = 22 * f(n-3) + 2 + 1 = 22 * (2f(n-4) + 1) = 23 * f(n-4) + 22 + 1 = .... // 不断地展开 = 2n-1 + 2n-2 + ....+ 1显然时间复杂度为O(2n),很明显指数级别的时间复杂度是不能接受的,汉诺塔非递归的解法比较复杂,大家可以去网上搜一下
进阶题实际面试中,很多递归题都不会用上面这些相对比较容易理解的题,更加地是对递归问题进行相应地变形,来看下面这道题
细胞分裂 有一个细胞 每一个小时分裂一次,一次分裂一个子细胞,第三个小时后会死亡。那么n个小时候有多少细胞?照例,我们用前面的递归四步曲来解
定义问题的递归函数,明确函数的功能 我们定义以下函数为n个小时后的细胞数
public int allCells(int n) { }接下来寻找问题与子问题间的关系(即递推公式)首先我们看一下一个细胞出生到死亡后经历的所有细胞分裂过程
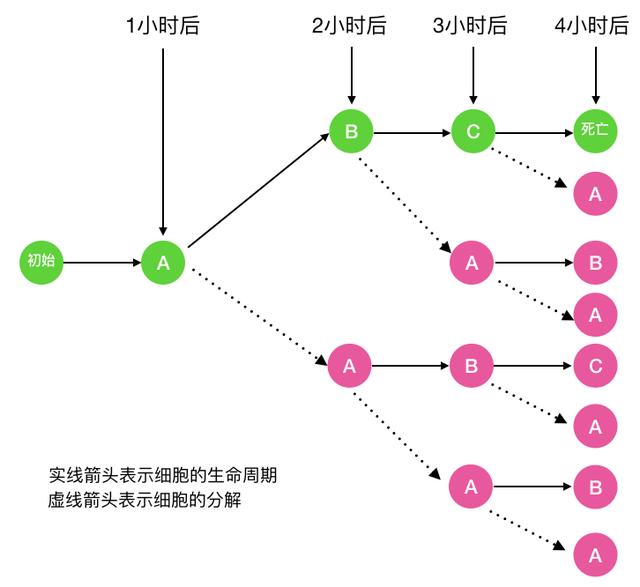
图中的A代表细胞的初始态, B代表幼年态(细胞分裂一次),C代表成熟态(细胞分裂两次),C再经历一小时后细胞死亡 以f(n)代表第n小时的细胞分解数fa(n) 代表第n小时处于初始态的细胞数,fb(n)代表第n小时处于幼年态的细胞数fc(n) 代表第 n 小时处于成熟态的细胞数 则显然 f(n) = fa(n) + fb(n) + fc(n) 那么 fa(n) 等于多少呢,以n = 4 (即一个细胞经历完整的生命周期)为例
仔细看上面的图,可以看出 fa(n)=fa(n-1) + fb(n-1) + fc(n-1), 当 n = 1 时,显然 fa(1) = 1
fb(n) 呢,看下图可知 fb(n) = fa(n-1)。当 n = 1 时 fb(n) = 0
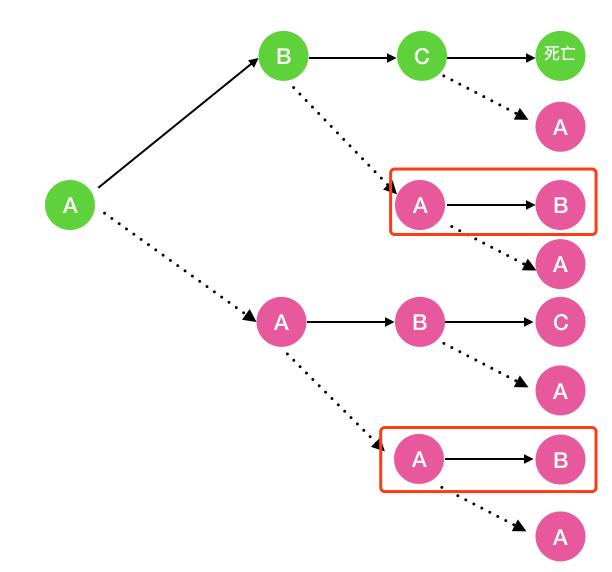
fc(n)呢,看下图可知 fc(n) = fb(n-1)。当n = 1,2 时fc(n) = 0
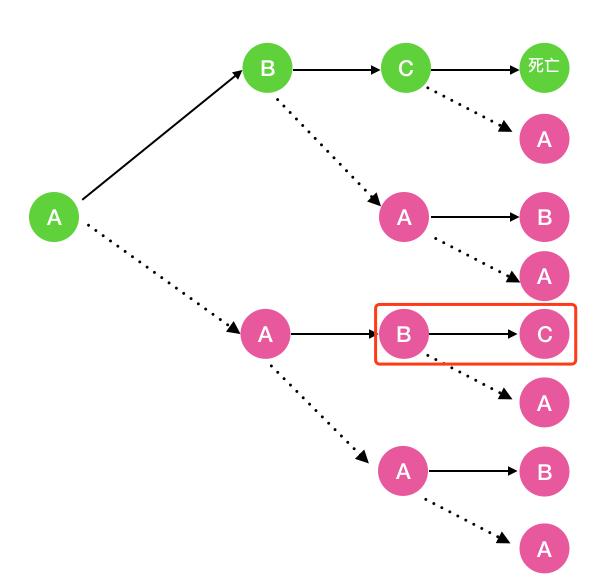
综上,我们得出的递归公式如下