最后也是很关键的一步,根据问题与子问题的关系,推导出时间复杂度,如果发现递归时间复杂度不可接受,则需转换思路对其进行改造,看下是否有更靠谱的解法
听起来是不是很简单,接下来我们就由浅入深地来看几道递归题,看下怎么用上面的几个步骤来套。
实战演练(从初级到高阶) 热身赛 输入一个正整数n,输出n!的值。其中n!=123…n,即求阶乘套用上一节我们说的递归四步解题套路来看看怎么解。
定义这个函数,明确这个函数的功能,我们知道这个函数的功能是求n的阶乘, 之后求n-1,n-2的阶乘就可以调用此函数了
/** * 求 n 的阶乘 */ public int factorial(int n) { }寻找问题与子问题的关系 阶乘的关系比较简单, 我们以 f(n) 来表示n的阶乘,显然f(n)= n * f(n - 1), 同时临界条件是 f(1) = 1,即
将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中
** * 求 n 的阶乘 */ public int factorial(int n) { // 第二步的临界条件 if (n < =1) { return 1; } // 第二步的递推公式 return n * factorial(n-1) }求时间复杂度 由于 f(n) = n * f(n-1) = n * (n-1) * .... * f(1),总共作了n次乘法,所以时间复杂度为 n。
看起来是不是有这么点眉目,当然这道题确实太过简单,很容易套路,那我们再来看进阶一点的题
入门题 一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,例如: 跳上第 1 级台阶只有一种跳法:直接跳 1 级即可。跳上第 2 级台阶 有两种跳法:每次跳 1 级,跳两次;或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法?定义一个函数,这个函数代表了跳上 n 级台阶的跳法
/** * 跳 n 极台阶的跳法 */ public int f(int n) { }寻找问题与子问题之前的关系 这两者之前的关系初看确实看不出什么头绪,但仔细看题目,一只青蛙只能跳一步或两步台阶,自上而下地思考,也就是说如果要跳到n级台阶只能从n-1 或n-2 级跳, 所以问题就转化为跳上n-1和n-2级台阶的跳法了,如果f(n)代表跳到n级台阶的跳法,那么从以上分析可得f(n)=f(n-1)+f(n-2),显然这就是我们要找的问题与子问题的关系,而显然当n=1,n=2,即跳一二级台阶是问题的最终解,于是递推公式系为
将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中 补充后的函数如下
/** * 跳 n 极台阶的跳法 */ public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; return f(n-1) + f(n-2) }计算时间复杂度 由以上的分析可知 f(n) 满足以下公式
斐波那契的时间复杂度计算涉及到高等代数的知识,这里不做详细推导,我们直接结出结论
由此可知时间复杂度是指数级别,显然不可接受,那回过头来看为啥时间复杂度这么高呢,假设我们要计算f(6),根据以上推导的递归公式,展示如下
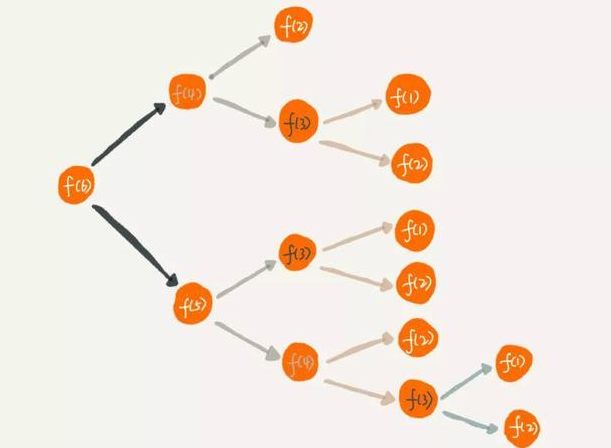
可以看到有大量的重复计算, f(3)计算了3次,随着n的增大,f(n)的时间复杂度自然呈指数上升了
优化
既然有这么多的重复计算,我们可以想到把这些中间计算过的结果保存起来,如果之后的计算中碰到同样需要计算的中间态,直接在这个保存的结果里查询即可,这就是典型的 以空间换时间,改造后的代码如下
public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; // map 即保存中间态的键值对, key 为 n,value 即 f(n) if (map.get(n)) { return map.get(n) } return f(n-1) + f(n-2) }那么改造后的时间复杂度是多少呢,由于对每一个计算过的f(n)我们都保存了中间态,不存在重复计算的问题,所以时间复杂度是O(n),但由于我们用了一个键值对来保存中间的计算结果,所以空间复杂度是 O(n)。问题到这里其实已经算解决了,但身为有追求的程序员,我们还是要问一句,空间复杂度能否继续优化?

