文章收录在公众号:bigsai 关注持续分享干货和资源
前言事情还要从一个故事讲起:
对于上面那只可爱的小狗狗不会,本篇即为该教程,首先,我要告诉这只可爱的小狗狗,这种问题你要使用的数据结构为优先队列,每次操作的时间复杂度为O(logn),而整个过程的时间复杂度为O(nlogn).
对于本片的设计与实现和堆排序可能有些相似,因为他们都借助堆来实现算法和数据结构,下面详细介绍优先队列的设计与实现。
堆而堆就是一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树(完全)的数组对象。且总是满足以下规则:
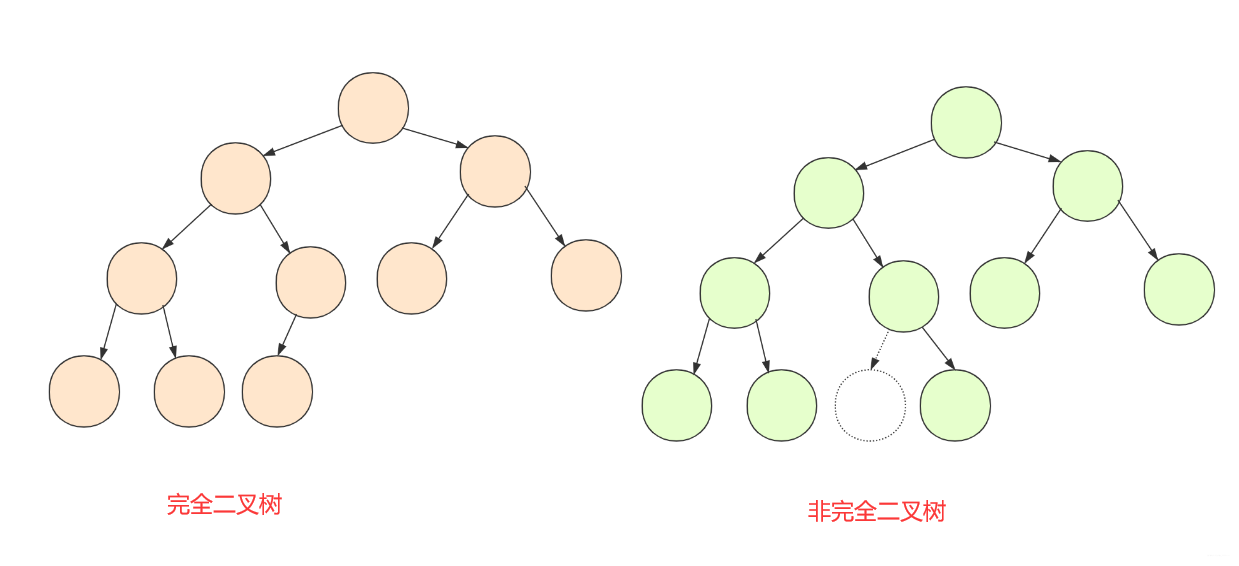
堆总是一棵完全二叉树
每个节点总是大于(或小于)它的孩子节点。
对于完全二叉树,我想大家都能明白,就是最底层叶子节点要严格按照从左向右来。
堆有大根堆和小根堆,如果是所有父节点都大于子节点的时候,那么这就是个大根堆,反之则为小根堆,以下就是一个大根堆:
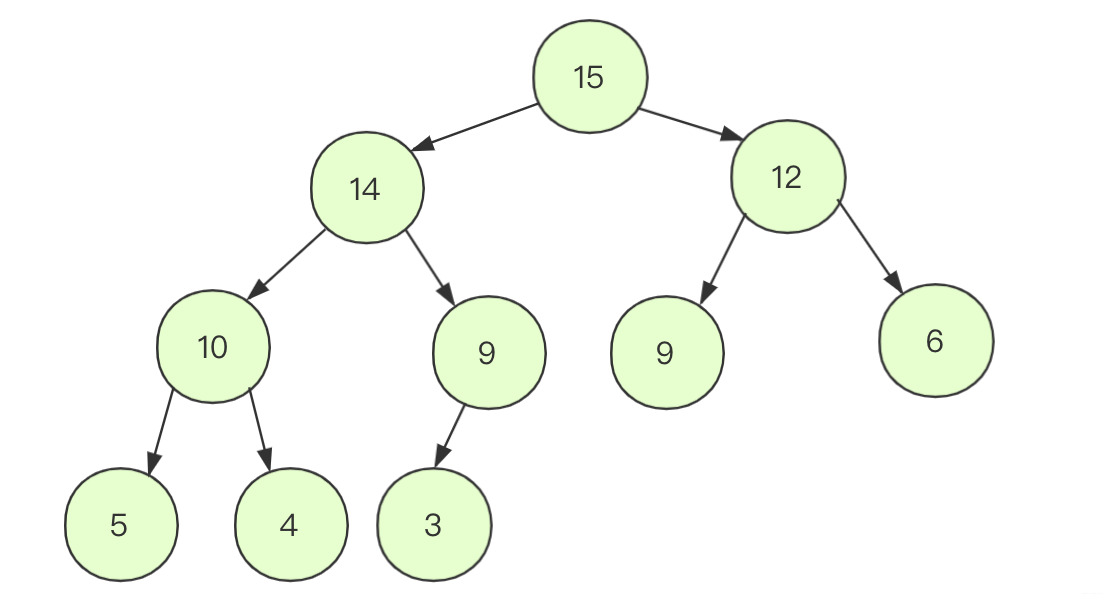
最后需要注意的是我们并不是用链式去储存这个二叉树而是用数组去存储这个树,虽然链式的使用场景可能更多一些,但是在完全二叉树的情况下空间使用率较好没有斜树的出现。并且在操作的时候可以直接通过编号找到位置进行交换。
优先队列
如何理解优先队列,我们先从一段对话说起:
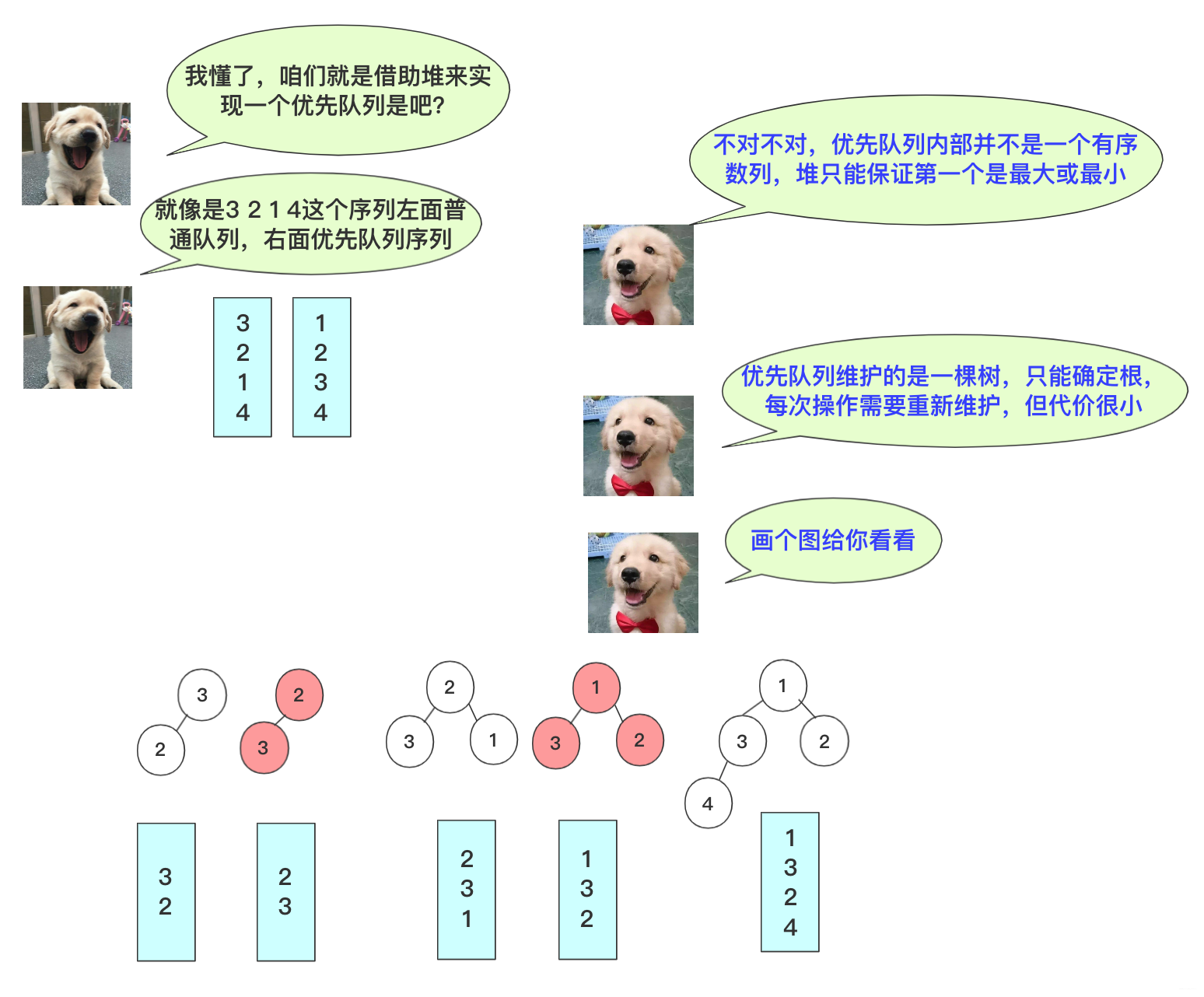
优先队列,它是一个队列。而普通的队列遵从先进先出的规则。而优先队列遵循一个排序的规则:每次抛出自定义排序最大(小)的,默认的情况是抛出最小的,本篇也就从最基本的原理进行分析。
并且它的用法队列还是一样的,,所以我们在设计这个类的时候api方面要与队列的api一致。
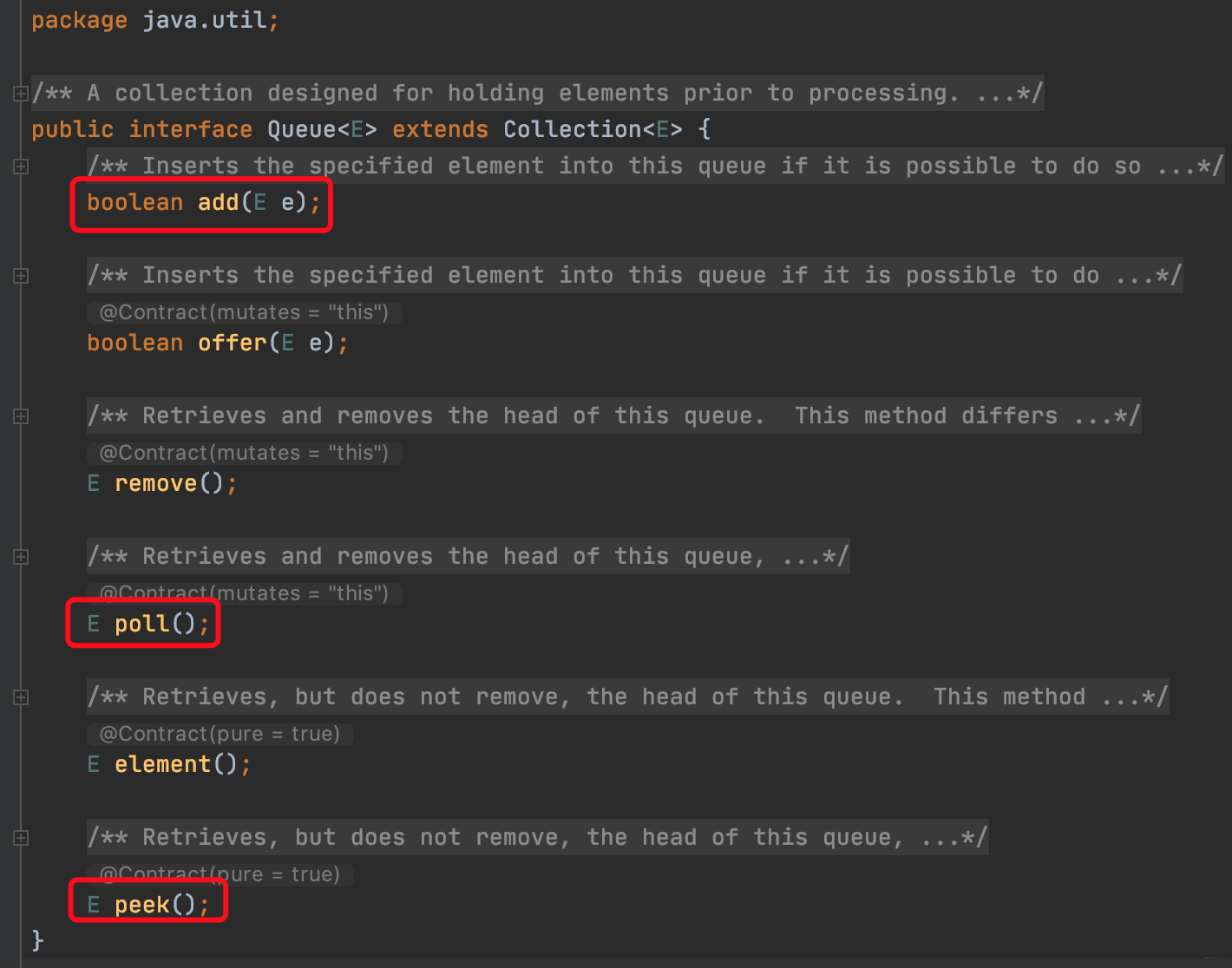
我们主要实现add、poll、和peek方法,并且会着重于算法的实现而不太着重一些细节的实现。
虽然优先队列和堆排序利用堆结构特性的流程有一些相似,但是两者其实还是有些操作上的区别的:
堆排序 :
刚开始是一个杂乱无章的序列,所以需要将杂乱的序列(树)通过一个方法变成一个合法的堆。
转成一个堆之后需要删除n次每次删除完都要重新调整这个堆。没有插入操作。
优先队列:
队列(堆)刚开始的内容为空,每次增加一个元素时需要即使调整堆。每次删除也要及时调整堆,增加和删除每次都只是一个元素。
但是优先队列的具体操作流程是如何的呢?我们具体分析其插入和删除的流程。
插入add流程(小根堆为例):
正常处理完的优先队列内的数据满足一个堆的结构,所以就是插入在堆中。
堆是一棵完全二叉树,所以在插入初始,插入到最后一个位置不影响其他结构。

