栈和排序 问题描述
给你一个由1~n,n个数字组成的一个排列和一个栈,要求按照排列的顺序入栈。如何在不打乱入栈顺序的情况下,仅利用入栈和出栈两种操作,输出字典序最大的出栈序列。
排列:指 1 到 n 每个数字出现且仅出现一次。
示例:
输入:[2,1,5,3,4]
输出:[5,4,3,1,2]
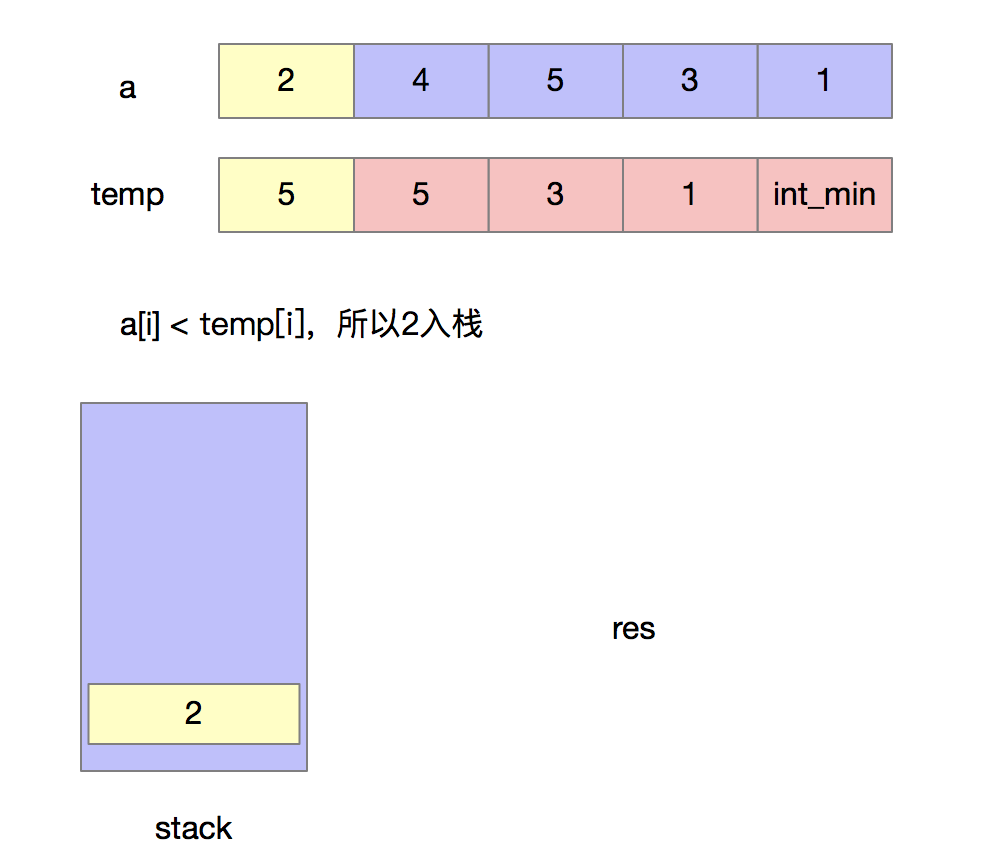
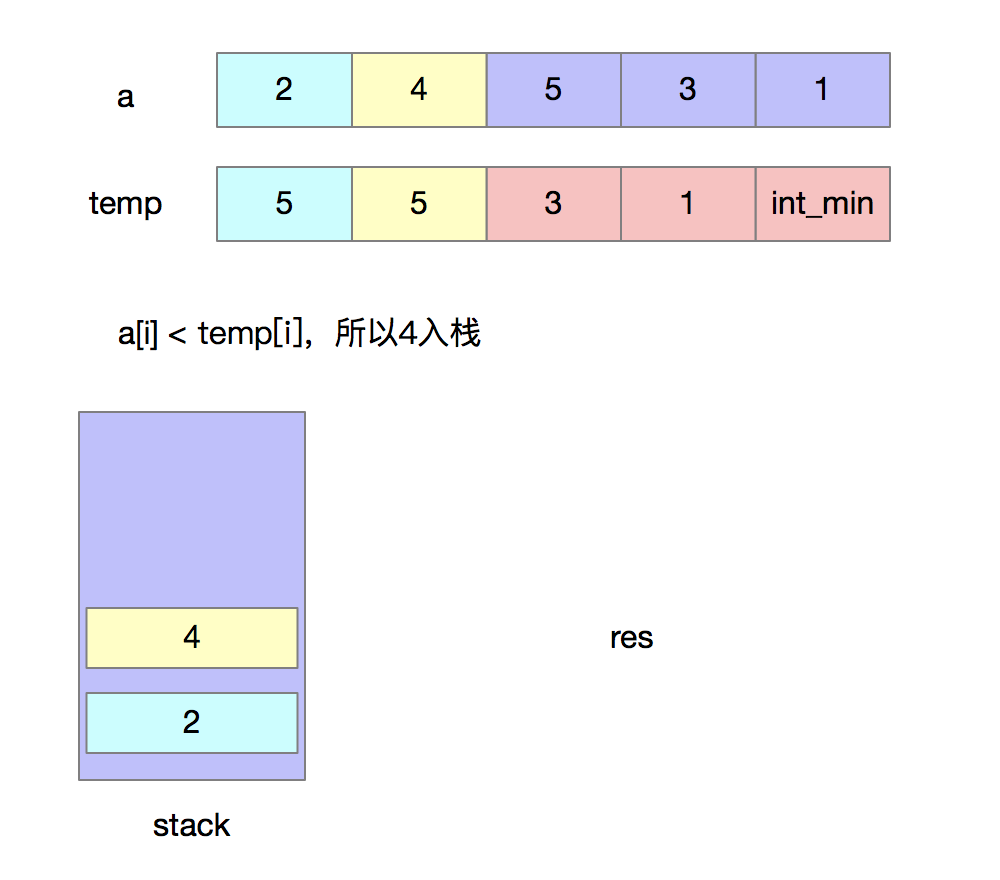
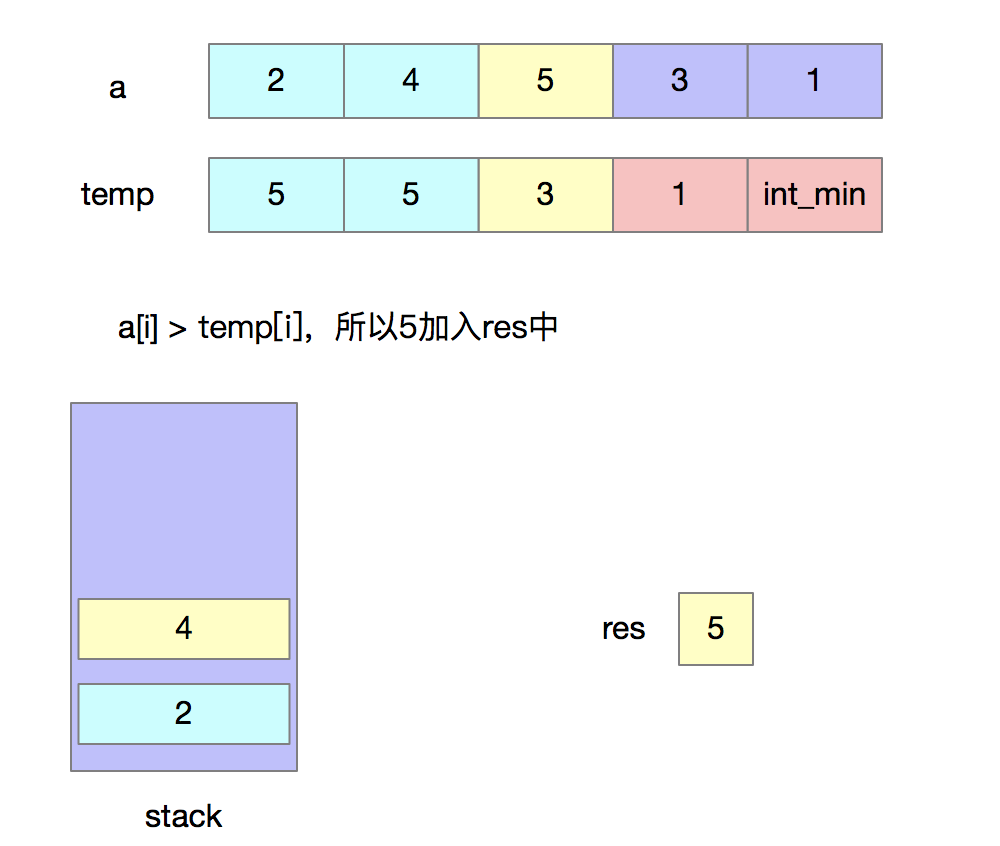
分析问题由于我们只能使用出栈和入栈两种操作,要想使得出栈序列字典序最大,首先想到的就是令高位尽可能地大,我们出栈的时机就是:当前入栈元素若是大于之后将要入栈的元素,那么就将其出栈。当元素出栈后,还需要判断栈顶元素与之后将要入栈元素之间的大小关系,如果此时栈顶元素大于之后将要入栈的元素,那么就将其出栈,不断判断直到栈为空或条件不满足。
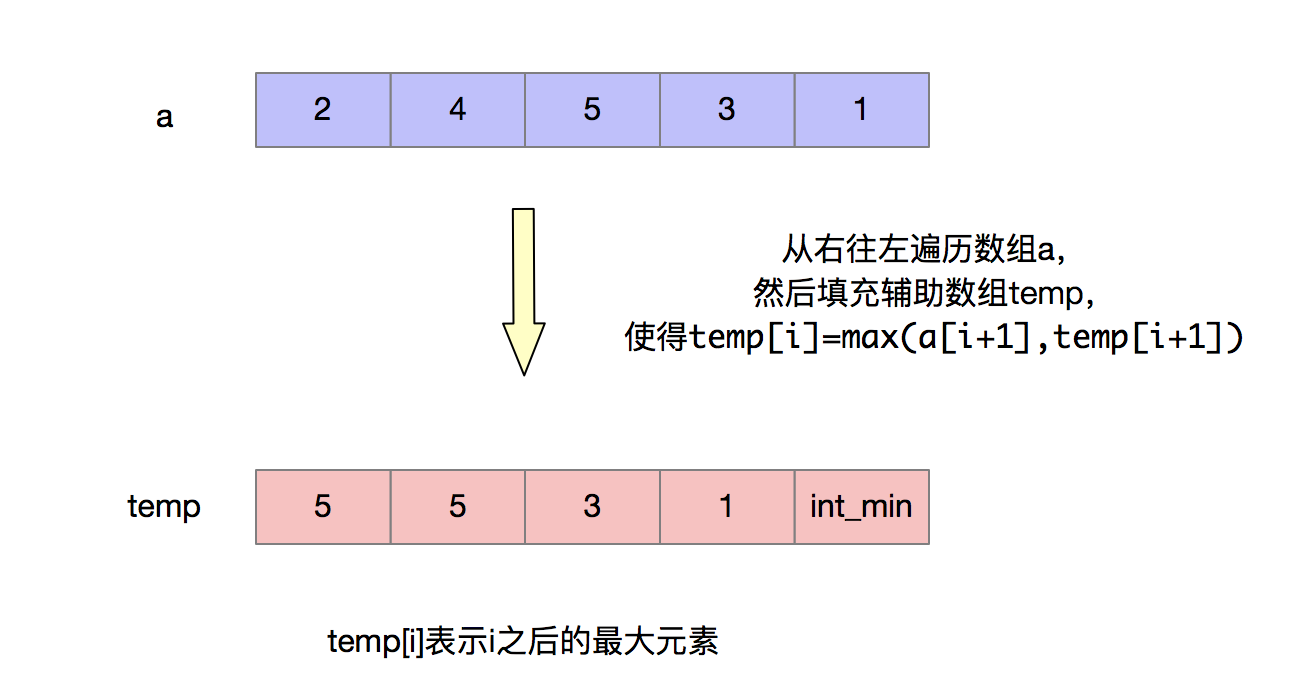
为了快速判断“当前入栈元素是否大于之后将要入栈的元素”,我们需要创建一个辅助数组temp,其中temp[i]表示i之后的最大元素。借助辅助数组,我们可以以O(1)的时间复杂度去判断当前入栈元素是否大于之后将要入栈的元素。
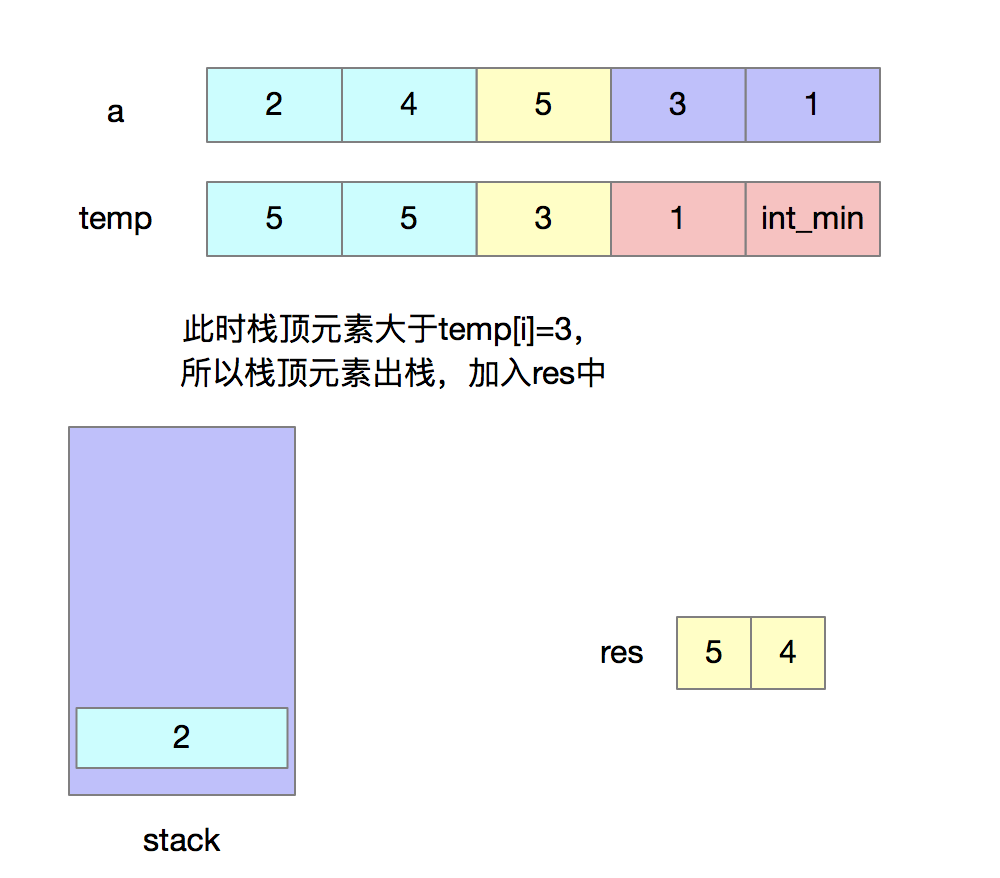
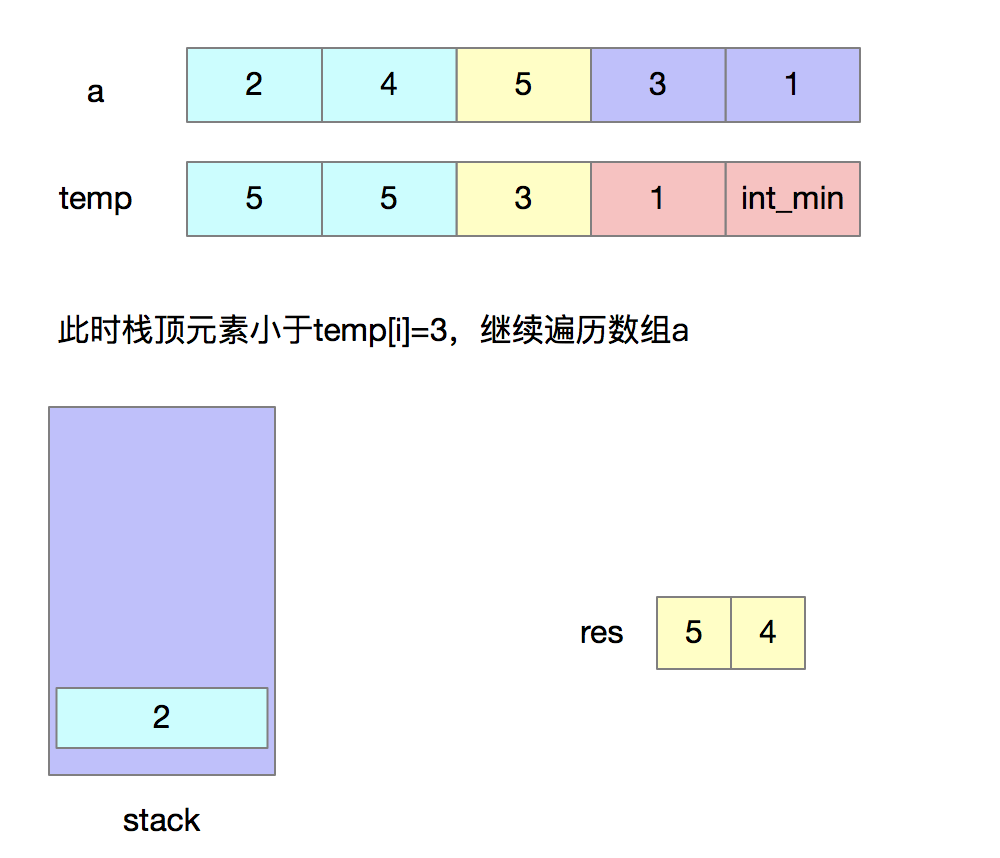
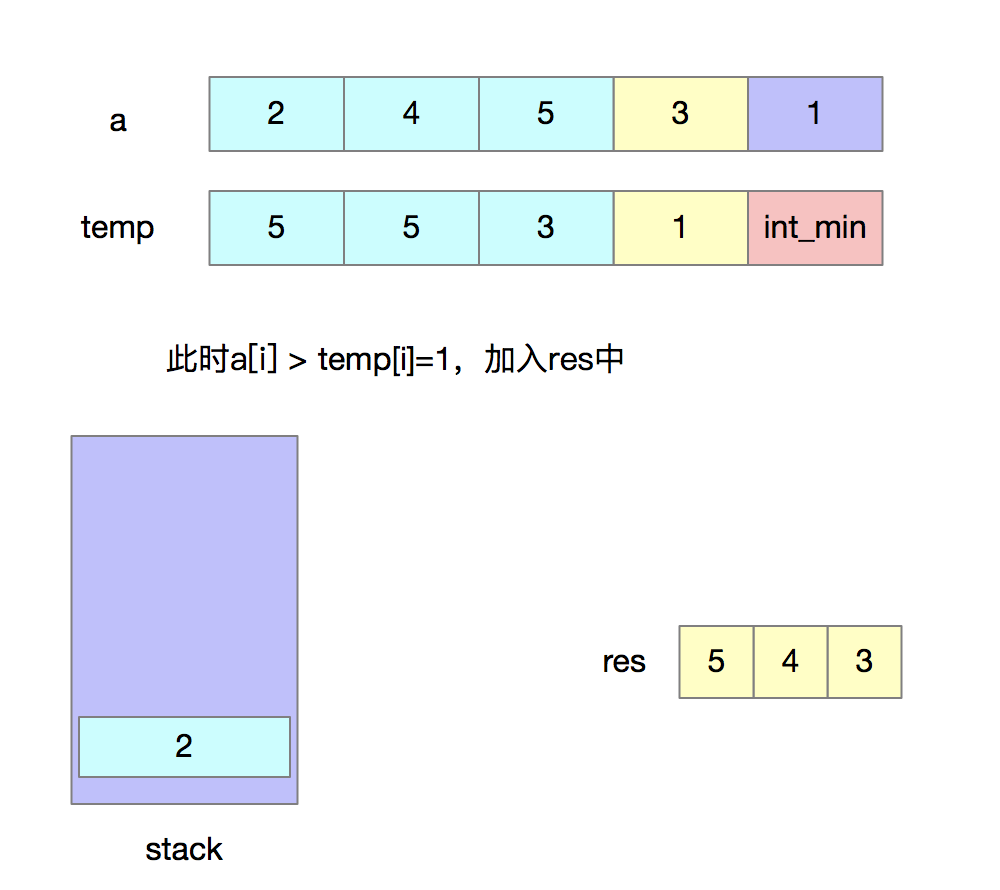
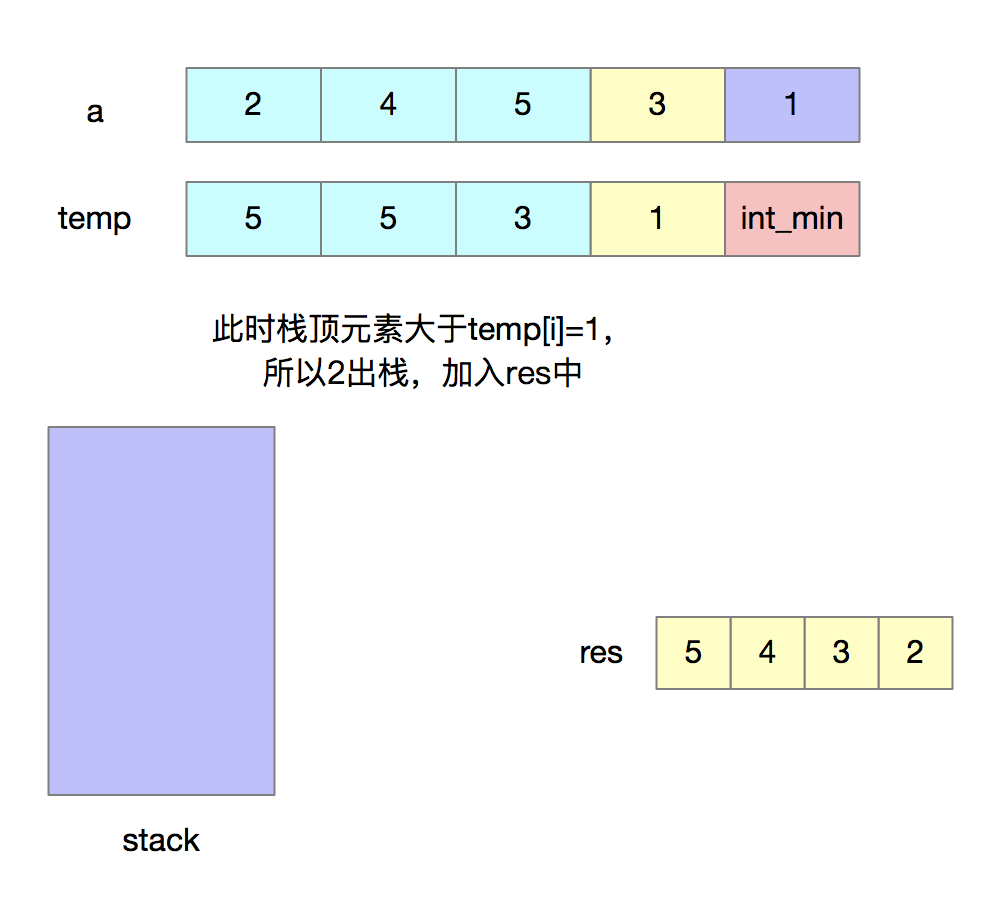
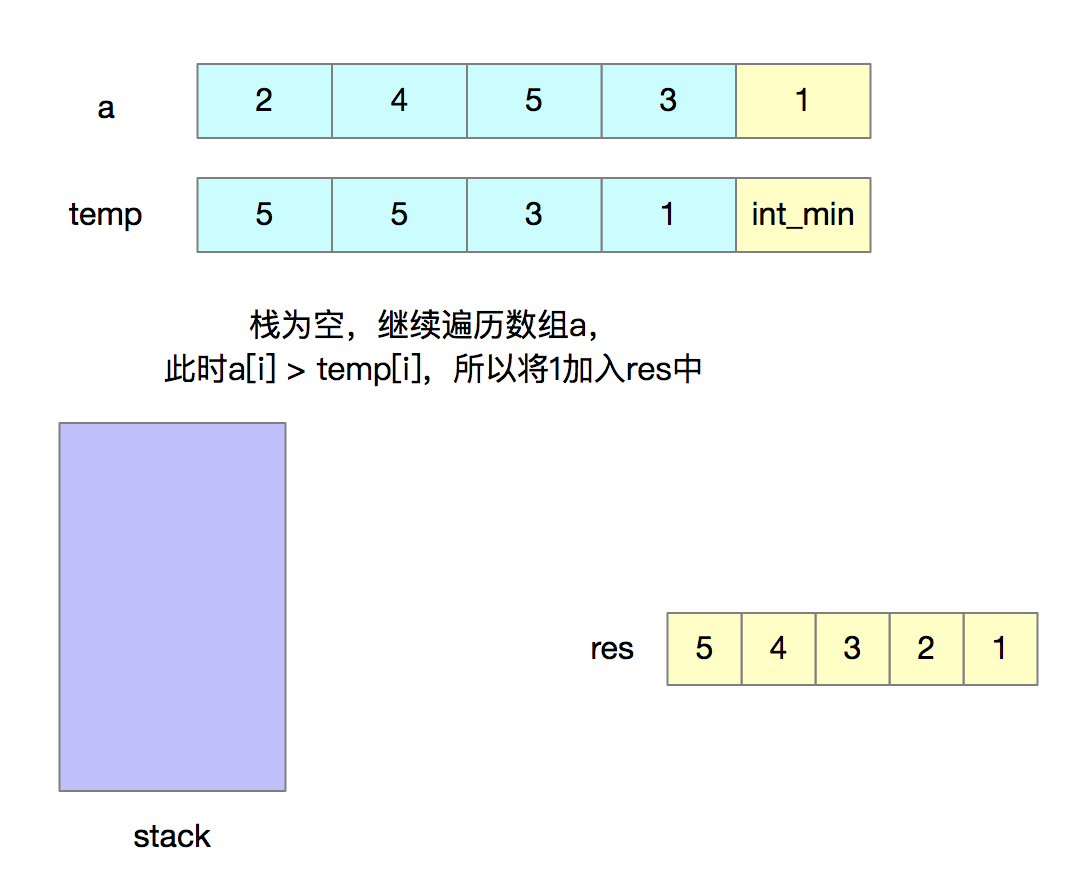
下面我们来看一下代码的实现。
import sys class Solution: def solve(self , a): n=len(a) res=[] if n==0: return res stack=[] temp=[0]*n temp[n-1]=-sys.maxsize-1 #从右往左遍历数组a,然后取填充temp #使得temp[i]表示i之后的最大元素 for i in range(n-2,-1,-1): temp[i]=max(a[i+1],temp[i+1]) #遍历数组a for i in range(0,n): if a[i] > temp[i]: #若当前元素大于之后将要入栈的元素,将其加入结果中 res.append(a[i]) # 若栈不为空,且栈顶元素大于temp[i], # 栈顶出栈,加入结果中 while stack and stack[-1] > temp[i]: res.append(stack[-1]) stack.pop() else: stack.append(a[i]) while stack: res.append(stack[-1]) stack.pop() return res该算法的时间复杂度是O(n),空间复杂度也是O(n)。

