这里S(X)=b(X)d(X),Xi是1~n之间的某个正整数,它表示在第i天晚上,被(首先)攻破的那个“元诱因”的编号,所以,X1、X2、…、Xm是独立同分布的随机变量,设该分布是p(x),于是有如下定理:
定理1若每天晚上黑客都将其全部资金按比例b=(b1,b2,…,bn)分配,来对系统的各“元诱因”进行攻击,那么,m天之后,黑客的资产就变为:
这里称为“双倍率”。
证明:由于独立随机变量的函数也是独立的,所以,也是独立同分布的,由弱大数定律,可得:
于是,证毕。
由于黑客的资产按照2mw(b,p)的方式增长(这也是把W(b,p)称为“双倍率”的根据),因此,只需要寻找某种资金分配战术b=(b1,b2,…,bn),使得双倍率W(b,p)最大即可。
定义1如果某种战术分配b,使得双倍率W(b,p)达到最大值W*(p),那么,就称该值为最优双倍率,即:
这里的最大值max是针对所有可能的满足而取的。
双倍率W(b,p)作为b的函数,在约束条件∑ni=1bi=1下,求其最大值。可以写出如下拉格朗日乘子函数并且改变对数的基底(这不影响最大化b),则有:
关于bi求导得到:
为了求得最大值,令偏导数为0,从而得出:
将它们带入约束条件可得到λ=-1和bi=pi。从而可知,b=p为函数J(b)的驻点。
定理2最优化双倍率

证明:将双倍率W(b,p)重新改写,使得容易看出何时取最大值:
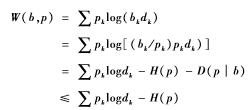
这里D(p|b)是随机变量p和b的相对熵[7]。而当b=p时,可直接验证上述等式成立。证毕。

