从定理2可知:对于一个可用离散随机变量X(Pr(X=i)= pi,并且,p1+p2+…+pn=1)来静态描述的黑客,他的动态最佳攻击战术也是(p1,p2,…,pn),即,将攻击资金按比例(p1,p2,…,pn)分配后,可得到最多的“黑产收入”。
下面再对定理2进行一些更细致的讨论,有:
定理3如果攻破每个“元诱因”的投入产出比是相同的,即,各个di彼此相等,都等于a,那么此时的最优化双倍率W*(p)=loga-H(p),即,最佳双倍率与熵之和为常数,并且,若按比例b*=p分配攻击资金,那么,此种战术的攻击业绩便可达到最大值。此时,第m天之后,黑客的财富变成而且,黑客的熵若减少1比特,那么,他的财富就会翻一倍!
如果并不知道每个di的具体值,而只知道∑1/di=1,此时,记ri=1/di,于是,双倍率可以重新写为:
由此可见双倍率与相对熵之间存在着非常密切的关系。
由于黑客每天晚上都要攻击系统,他一定会总结一些经验来提高攻击效果。更准确地说,可以假设黑客知道了攻破系统的某种边信息Y,它也是一个随机变量。
设X∈{1,2,…,n}为第X个“元诱因”,攻破它的概率为p(x),而攻击它的投入产出比为d(x)。设(X,Y)的联合概率密度函数为p(x,y)。用b(x|y)≥0,∑xb(x|y)=1记为已知边信息Y的条件下,黑客对攻击资金的分配比例。此处b(x|y)理解为:当得知信息y的条件下,用来攻击第x个“元诱因”的资金比例。对照前面的记号,将b(x)≥0,表示为无条件下,黑客对攻击资金的分配比例。
设无条件双倍率和条件双倍率分别为:
对于独立同分布的“攻击元诱因”序列(Xi,Yi),可以看到:当具有边信息Y时,黑客的相对收益增长率为2mw(X|Y);当黑客无边信息时,他的相对收益增长率为2mw(X)。
定理4由于获得攻击“元诱因”X的边信息Y,而引起的双倍率增量ΔW满足ΔW=I(X;Y)。这里I(X;Y)是随机变量X和Y的互信息。
证明:在有边信息的条件下,按照条件比例分配攻击资金,即,b*(x|y)=p(x|y),那么关于边信息Y的条件双倍率W(X|Y)可以达到最大值。于是:
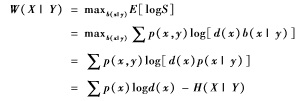
当无边信息时,最优双倍率为:
从而,由于边信息Y的存在,而导致的双倍率的增量为:
证毕。
此处双倍率的增量正好是边信息Y与“元诱因”X之间的互信息。因此,如果边信息Y与“元诱因”X相互独立,那么,双倍率的增量就为0。
设Xk是黑客第k天攻破的“元诱因”的序号,假如各{Xk}之间不是独立的,又假设每个dk彼此相同,都等于a。于是,黑客根据随机过程{Xk}来决定第(k+1)天的最佳攻击资金分配方案(即最佳双倍率)为:
这里的最大值max是针对所有满足如下条件的边信息攻击资金分配方案而取的:

