选择排序的思路很简单,实现起来也不难。
public void sort(int[] nums) { int min = 0; for (int i = 0; i < nums.length - 1; i++) { for (int j = i + 1; j < nums.length; j++) { //寻找最小的数 if (nums[j] < min) { min = j; } } //交换 int temp = nums[i]; nums[i] = nums[min]; nums[min] = temp; } } 选择排序性能分析选择排序稳定吗?
答案是不稳定的,因为在未排序序列中找到最小值之后,和排序序列的末尾元素交换。
算法名称 最好时间复杂度 最坏时间复杂度 平均时间复杂度 空间复杂度 是否稳定选择排序 O(n²) O(n²) O(n²) O(1) 不稳定
插入排序 插入排序原理
关于插入排序,有一个非常形象的比喻。斗地主——摸到的牌都是乱的,我们会把摸到的牌插到合适的位置。
它的思路:将一个元素插入到已经排好序的有序序列中,从而得到一个新的有序序列。
动图如下(来源参考3):
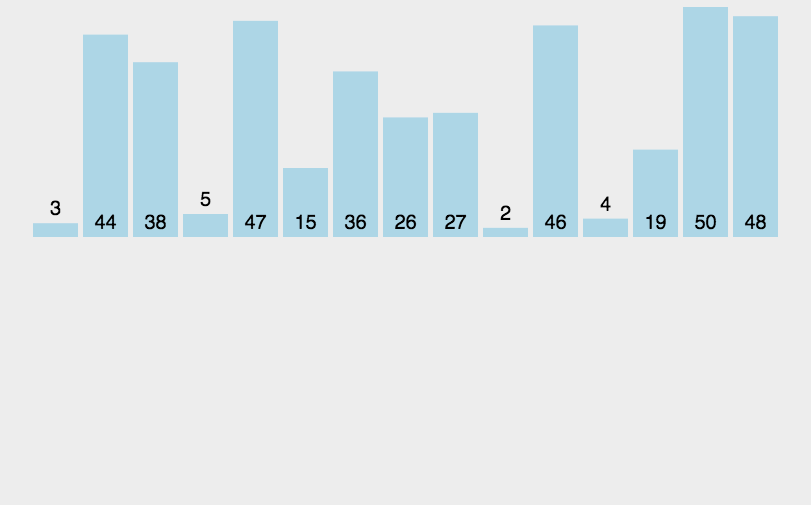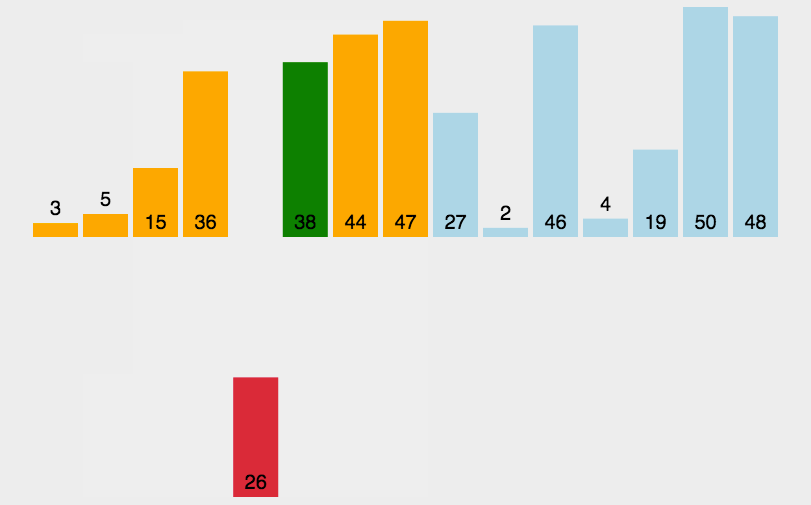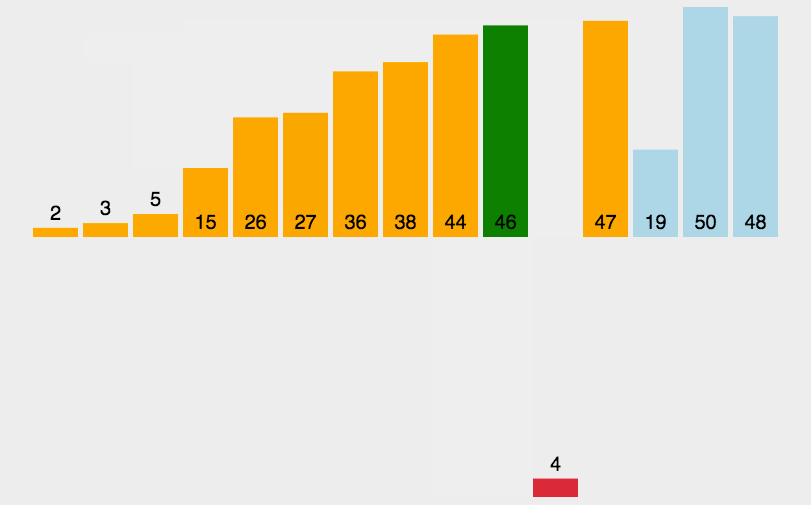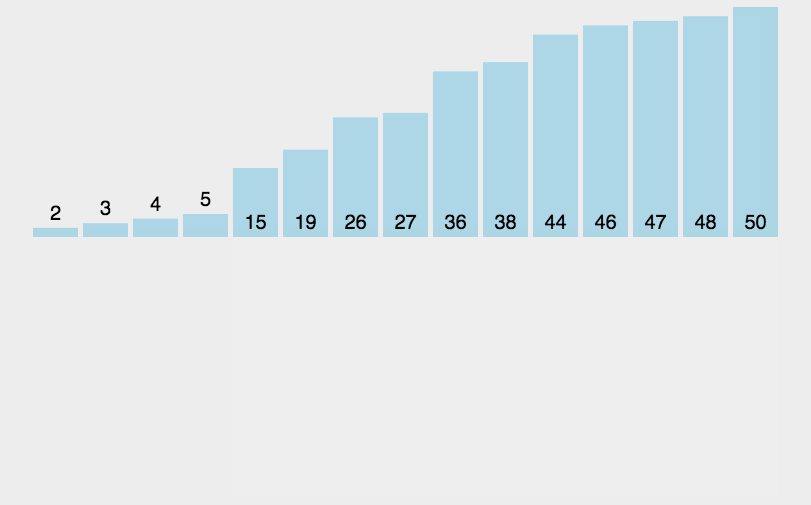
还是以数组 [2,5,4,1,3]为例:
第一趟:从未排序的序列将元素5插入到已排序的序列的合适位置

第二趟:接着从未排序的序列中,将元素4插入到已经排序的序列的合适位置,需要遍历有序序列,找到合适的位置

第三趟:继续,把1插入到合适的位置

第五趟:继续,把3插入到合适的位置

OK,排序结束。
插入排序代码实现找到插入元素的位置,移动其它元素。
public void sort(int[] nums) { //无序序列从1开始 for (int i = 1; i < nums.length; i++) { //需要插入有序序列的元素 int value = nums[i]; int j = 0; for (j = i - 1; j >= 0; j--) { //移动数据 if (nums[j] > value) { nums[j + 1] = nums[j]; } else { break; } } //插入元素 nums[j + 1] = value; } } 插入排序性能分析插入排序智慧移动比插入元素大的元素,所以相同元素相对位置不变,是稳定的。
从代码里我们可以看出,如果找到了合适的位置,就不会再进行比较了,所以最好情况时间复杂度是O(n)。
算法名称 最好时间复杂度 最坏时间复杂度 平均时间复杂度 空间复杂度 是否稳定插入排序 O(n) O(n²) O(n²) O(1) 稳定
希尔排序 希尔排序原理
希尔排序,名字来自它的发明者Shell。它是直接插入排序的改进版。
希尔排序的思路是:把整个待排序的记录序列分割成若干个子序列,分别进行插入排序。
我们知道直接插入排序在面对大量无序数据的时候不太理想,希尔排序就是通过跳跃性地移动,来达到数组元素地基本有序,再接着用直接插入排序。
希尔排序动图(动图来源参考[1]):

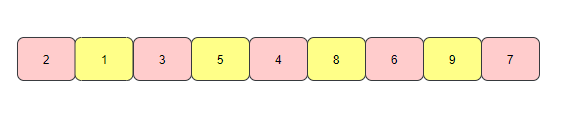
还是以数组 [2,5,6,1,7,9,3,8,4]为例,我们来看一下希尔排序的过程:
数组元素个数为9,取7/2=4为下标差值,将下标差值为4的元素分为一组

组内进行插入排序,构成有序序列

再取4/2=2为 下标差值,将下标差值为2的元素分为一组

组内插入排序,构成有序序列
下标差值=2/2=1,将剩余的元素插入排序

可以看看前面的插入排序,希尔排序
只是一个有步长的直接插入排序。
public void sort(int[] nums){ //下标差 int step=nums.length; while (step>0){ //这个是可选的,也可以是3 step=step/2; //分组进行插入排序 for (int i=0;i<step;i++){ //分组内的元素,从第二个开始 for (int j=i+step;j<nums.length;j+=step){ //要插入的元素 int value=nums[j]; int k; for (k=j-step;k>=0;k-=step){ if (nums[k]>value){ //移动组内元素 nums[k+step]=nums[k]; }else { break; } } //插入元素 nums[k+step]=value; } } } } 希尔排序性能分析稳定度分析

