万字长文|十大基本排序，一次搞定！ (7)

桶排序最好的情况，就是元素均匀分配到了每个桶，时间复杂度O(n)，最坏情况，是所有元素都分配到一个桶中，时间复杂度是O(n²)。平均的时间复杂度和技术排序一样，都是O(n+k)。

空间复杂度

桶排序，需要存储n个额外的桶，桶中又要存储k个元素，所以空间复杂度是O(n+k)。

稳定性

稳定性得看桶中排序用的什么排序算法，桶中用的稳定排序算法，那么就是稳定的。用的不稳定的排序算法，那么就是不稳定的。

基数排序 基数排序原理

基数排序是一种非比较型的排序方法。

它的基本原理是将元素按照位数切割成不同的数字，然后按照每个位数进行比较。

大概过程：

取得数组中的最大数，并取得位数；

arr为原始数组，从最低位开始取每个位组成radix数组

对radix进行计数排序（利用计数排序适用于小范围数的特点）

动图图示如下（来源参考[1]）：

基数排序可以说是桶排序的一个进化，我们以 [ 892， 846， 821， 199， 810，700 ]来看一下基数排序的过程：

创建十个桶用来存储元素

根据个位数，将元素分别分配到不同的桶中

然后将桶中的元素依次取出

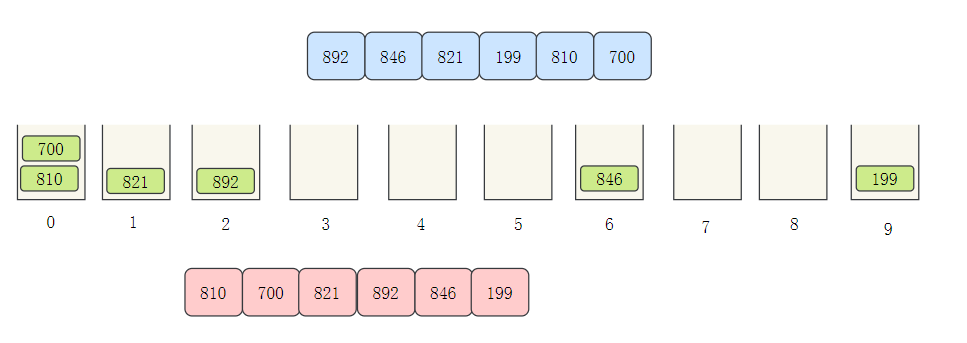
接下来排十位数，根据十位数分配桶，再依次取出

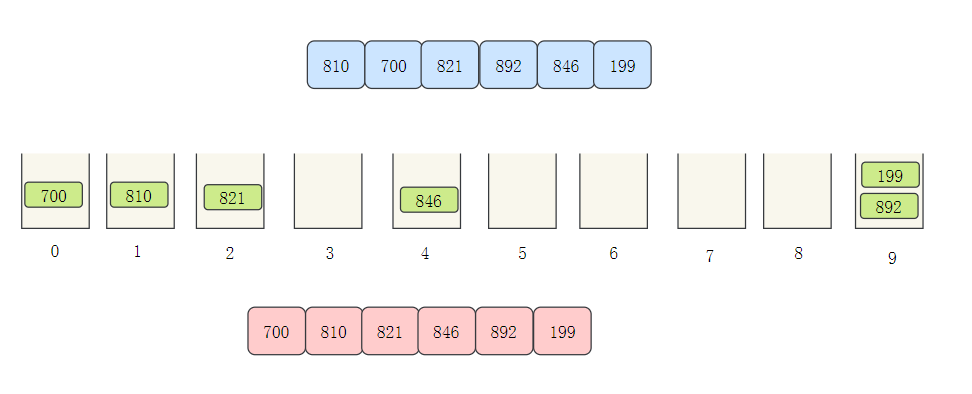
接下来百位数

基数排序代码实现 public class RadixSort { public void sort(int[] nums) { int len = nums.length; //最大值 int max = nums[0]; for (int i = 0; i < len; i++) { if (nums[i] > max) { max = nums[i]; } } //当前排序位置 int location = 1; //用列表实现桶 List<List<Integer>> buckets = new ArrayList<>(); //初始化size为10的一个桶 for (int i = 0; i < 10; i++) { buckets.add(new ArrayList<>()); } while (true) { //元素最高位数 int d = (int) Math.pow(10, (location - 1)); //判断是否排完 if (max < d) { break; } //数据入桶 for (int i = 0; i < len; i++) { //计算余数 放入相应的桶 int number = ((nums[i] / d) % 10); buckets.get(number).add(nums[i]); } //写回数组 int nn = 0; for (int i = 0; i < 10; i++) { int size = buckets.get(i).size(); for (int ii = 0; ii < size; ii++) { nums[nn++] = buckets.get(i).get(ii); } buckets.get(i).clear(); } location++; } } } 基数排序性能分析

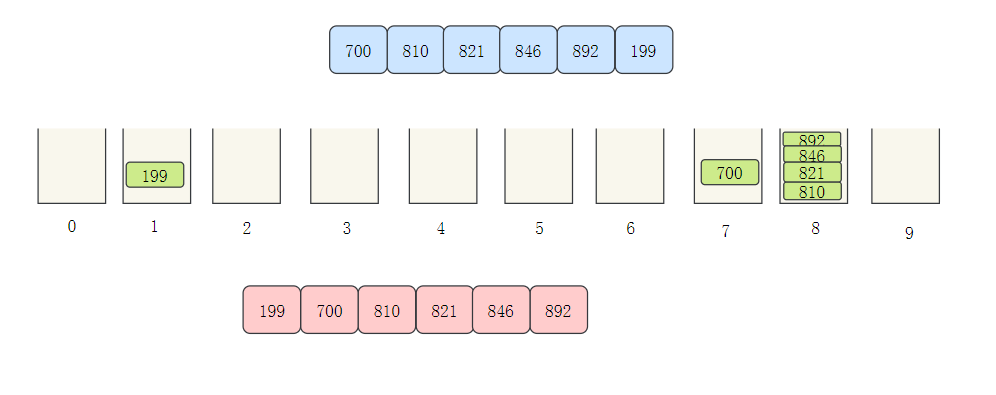
时间复杂度

时间复杂度O(n+k)，其中n数组元素个数，k为数组元素最高位数。

空间复杂度

和桶排序一样，因为引入了桶的存储空间，所以空间复杂度O(n+k)。

稳定性

因为基数排序过程，每次都是将当前位数是哪个相同数值的元素统一分配到桶中，并不交换位置，所以基数排序是稳定的。

总结

这篇文章，我们学习了十大基本排序，来简单总结一下。

首先最简单的冒泡排序：两层循环，相邻交换；

选择排序：未排序和排序两分，从未排序序列中寻找最小的元素，放在排序序列末尾；

插入排序：斗地主摸牌思维，把一个元素插入到有序序列合适位置；

希尔排序：插入排序plus，先把序列分割，再分别插入排序；

归并排序：分治思想第一弹，先将序列切分，再在合并过程排序；

快速排序：分治思想第二弹，基准数分区原序列，小的放左边，大的放右边；

堆排序：选择排序plus，建立大顶堆，堆顶元素（最大值）插入序列末尾，再让新的元素上浮。

计数排序：空间换时间第一弹，利用新数组，统计对应元素出现次数，输出新数组下标，原数组完成排序；

桶排序：空间换时间第二弹，将原数组的元素分到若干个桶，每个桶单独排序，再把桶里元素拼起来；

基数排序：空间换时间第三弹，桶排序plus，根据数位，把元素分桶，然后按每个位数比较。

十大基本排序性能汇总：

排序方法 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度 稳定性
冒泡排序   O(n²)   O(n²)   O(n)   O(1)   稳定  
选择排序   O(n²)   O(n²)   O(n²)   O(1)   不稳定  
插入排序   O(n²)   O(n²)   O(n)   O(1)   稳定  
希尔排序   O(n^(1.3-2))   O(n²)   O(n)   O(1)   不稳定  
归并排序   O(nlogn)   O(nlogn)   O(nlogn)   O(n)   稳定  
快速排序   O(nlogn)   O(n²)   O(nlogn)   O(nlogn)   不稳定  
堆排序   O(nlogn)   O(nlogn)   O(nlogn)   O(1)   不稳定  
计数排序   O(n+k)   O(n+k)   O(n+k)   O(n)   稳定  
桶排序   O(n+k)   O(n²)   O(n)   O(n+k)   稳定  
基数排序   O(n*k)   O(n*k)   O(n*k)   O(n+k)   稳定  

简单的事情重复做，重复的事情认真做，认真的事情有创造性地去做。

我是三分恶，一个能文能武的全栈开发。

点赞、关注 不迷路，咱们下期见！

参考：

[1].这或许是东半球分析十大排序算法最好的一篇文章

[2]. https://github.com/chefyuan/algorithm-base

[2].《数据结构与算法分析》

[3]. 面试高频：Java常用的八大排序算法一网打尽！

[4]. 十大经典排序算法（动图演示）

[5]. 剖析JDK8中Arrays.sort底层原理及其排序算法的选择