万字长文|十大基本排序，一次搞定！ (5)

上面的动图，使用的就是下沉的方式。

堆排序代码实现 public class HeapSort { public void sort(int[] nums) { int len = nums.length; //建堆 buildHeap(nums, len); for (int i = len - 1; i > 0; i--) { //将堆顶元素和堆末元素调换 swap(nums, 0, i); //数组计数长度减1，隐藏堆尾元素 len--; //将堆顶元素下沉，使最大的元素浮到堆顶来 sink(nums, 0, len); } } /** * 建堆 * * @param nums * @param len */ public void buildHeap(int[] nums, int len) { for (int i = len / 2; i >= 1; i--) { //下沉 sink(nums, i, len); } } /** * 下沉操作 * * @param nums * @param index * @param end */ public void sink(int[] nums, int index, int end) { //左子节点下标 int leftChild = 2 * index + 1; //右子节点下标 int rightChild = 2 * index + 2; //要调整的节点下标 int current = index; //下沉左子树 if (leftChild < end && nums[leftChild] > nums[current]) { current = leftChild; } //下沉右子树 if (rightChild < end && nums[rightChild] > nums[current]) { current = rightChild; } //如果下标不相等，证明调换过了 if (current!=index){ //交换值 swap(nums,index,current); //继续下沉 sink(nums,current,end); } } public void swap(int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } } 堆排序性能分析

时间复杂度

堆排的时间复杂度和快排的时间复杂度一样，都是O(nlogn)。

空间复杂度

堆排没有引入新的空间，原地排序，空间复杂度O(1)。

稳定性

堆顶的元素不断下沉，交换，会改变相同元素的相对位置，所以堆排是不稳定的。

算法名称 时间复杂度 空间复杂度 是否稳定
堆排序   O(nlogn)   O(1)   不稳定  
计数排序

文章开始我们说了，排序分为比较类和非比较类，计数排序是一种非比较类的排序方法。

计数排序是一种线性时间复杂度的排序，利用空间来换时间，我们来看看计数排序是怎么实现的吧。

计数排序原理

计数排序的大致过程[4]：

找出待排序的数组中最大和最小的元素

统计数组中每个值为i的元素出现的次数，存入数组arr的第i项；

对所有的计数累加（从arr中的第一个元素开始，每一项和前一项相加）；

反向填充目标数组：将每个元素i放在新数组的第arr(i)项，每放一个元素就将arr(i)减去1。

我们看一下动图演示（来自参考[4]）：

我们拿一个数组来看一下完整过程：[6,8,5,1,2,2,3]

首先，找到数组中最大的数，也就是8，创建一个最大下标为8的空数组arr

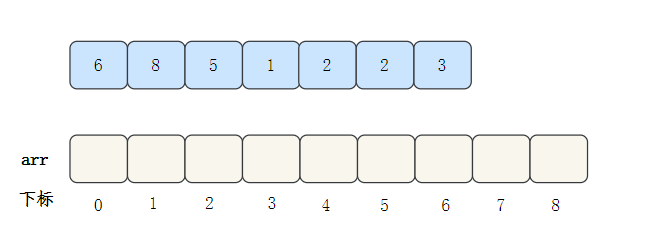
遍历数据，将数据的出现次数填入arr对应的下标位置中

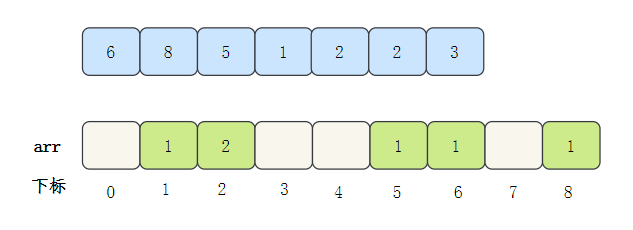
然后输出数组元素的下标值，元素的值是几，就输出几次

计数排序代码实现 public class CountSort { public void sort(int[] nums) { //查找最大值 int max = findMax(nums); //创建统计次数新数组 int[] countNums = new int[max + 1]; //将nums元素出现次数存入对应下标 for (int i = 0; i < nums.length; i++) { int num = nums[i]; countNums[num]++; nums[i] = 0; } //排序 int index = 0; for (int i = 0; i < countNums.length; i++) { while (countNums[i] > 0) { nums[index++] = i; countNums[i]--; } } } public int findMax(int[] nums) { int max = nums[0]; for (int i = 0; i < nums.length; i++) { if (nums[i] > max) { max = nums[i]; } } return max; } }

OK，乍一看没啥问题，但是仔细想想，其实还是有些毛病的，毛病在哪呢？

如果我们要排序的元素有0怎么办呢？例如[0,0,5,2,1,3,4] ，arr初始都为0，怎么排呢？

这个很难解决，有一种办法，就是计数的时候原数组先加10，[-1,0,2]，排序写回去的时候再减，但是如果刚好碰到有-10这个元素就凉凉。

如果元素的范围很大呢？例如[9992,9998,9993,9999]，那我们申请一个10000个元素的数组吗？