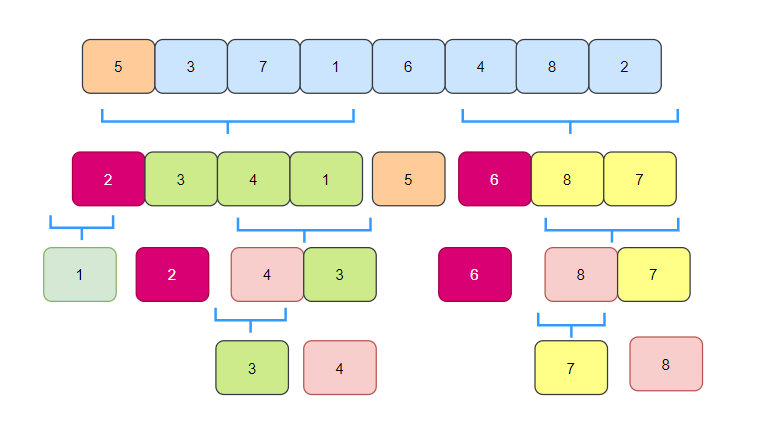
希尔排序是直接插入排序的变形,但是和直接插入排序不同,它进行了分组,所以不同组的相同元素的相对位置可能会发生改变,所以它是不稳定的。
时间复杂度分析
希尔排序的时间复杂度跟增量序列的选择有关,范围为 O(n^(1.3-2)) 在此之前的排序算法时间复杂度基本都是 O(n²),希尔排序是突破这个时间复杂度的第一批算法之一。
算法名称 时间复杂度 空间复杂度 是否稳定希尔排序 O(n^(1.3-2)) O(1) 不稳定
归并排序 归并排序原理
归并排序是建立在归并操作上的一种有效的排序算法,归并,就是合并的意思,在数据结构上的定义就是把把若干个有序序列合并成一个新的有序序列。
归并排序是分治法的典型应用,分治什么意思呢?就是把一个大的问题分解成若干个小的问题来解决。
归并排序的步骤,是把一个数组切分成两个,接着递归,一直到单个元素,然后再合并,单个元素合并成小数组,小数组合并成大数组。
动图如下(来源参考[4]):
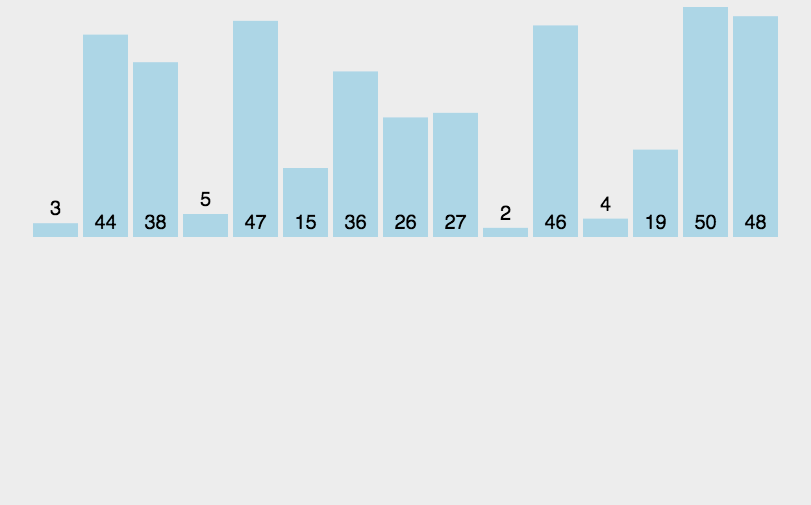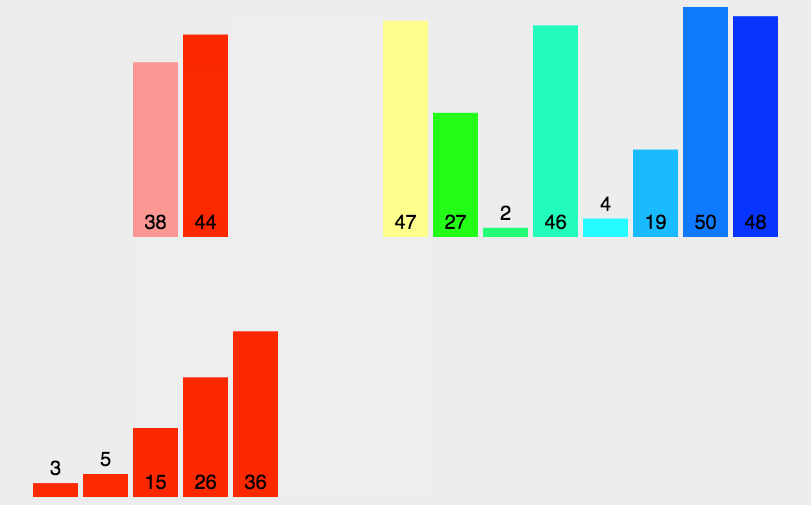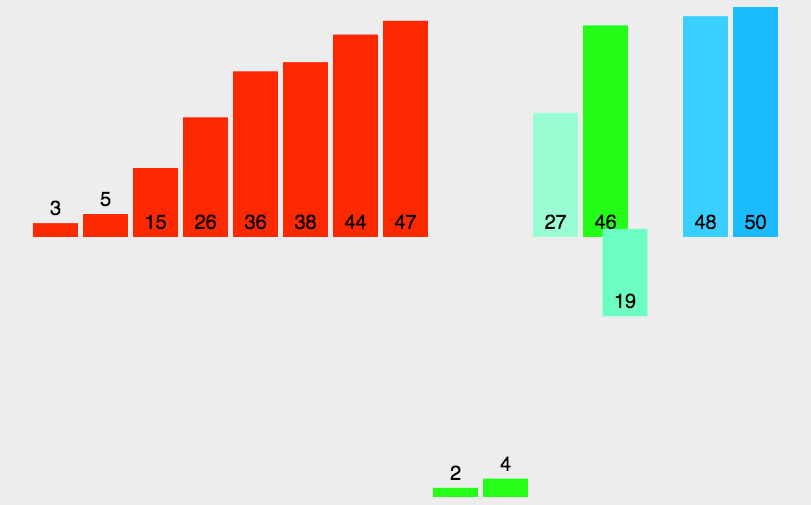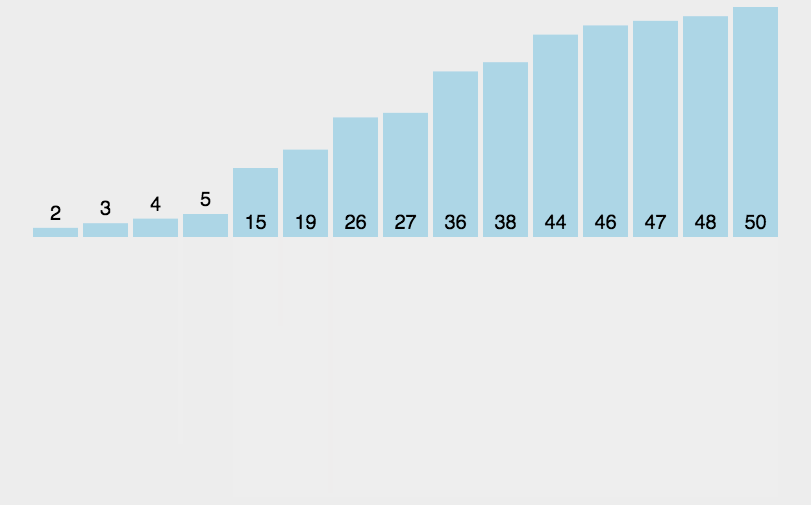
我们以数组[2,5,6,1,7,3,8,4] 为例,来看一下归并排序的过程:
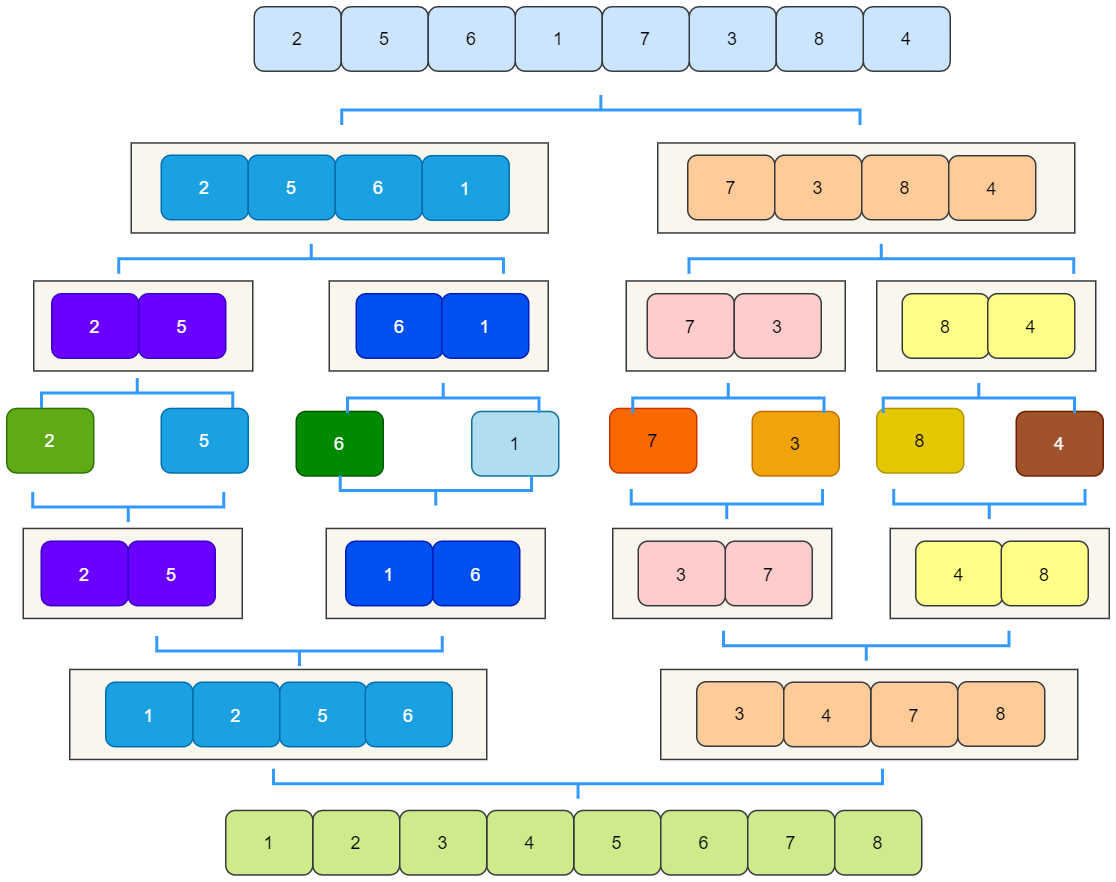
拆分就不用多讲了,我们看看怎么合并。
归并排序代码实现这里使用递归来实现归并排序:
递归终止条件
递归起始位置小于终止位置
递归返回结果
直接对传入的数组序列进行排序,所以无返回值
递归逻辑
将当前数组分成两组,分别分解两组,最后归并
代码如下:
public class MergeSort { public void sortArray(int[] nums) { sort(nums, 0, nums.length - 1); } /** * 归并排序 * * @param nums * @param left * @param right */ public void sort(int[] nums, int left, int right) { //递归结束条件 if (left >= right) { return; } int mid = left + (right - left) / 2; //递归当前序列左半部分 sort(nums, left, mid); //递归当前序列右半部分 sort(nums, mid + 1, right); //归并结果 merge(nums, left, mid, right); } /** * 归并 * * @param arr * @param left * @param mid * @param right */ public void merge(int[] arr, int left, int mid, int right) { int[] tempArr = new int[right - left + 1]; //左边首位下标和右边首位下标 int l = left, r = mid + 1; int index = 0; //把较小的数先移到新数组中 while (l <= mid && r <= right) { if (arr[l] <= arr[r]) { tempArr[index++] = arr[l++]; } else { tempArr[index++] = arr[r++]; } } //把左边数组剩余的数移入数组 while (l <= mid) { tempArr[index++] = arr[l++]; } //把右边剩余的数移入数组 while (r <= right) { tempArr[index++] = arr[r++]; } //将新数组的值赋给原数组 for (int i = 0; i < tempArr.length; i++) { arr[i+left] = tempArr[i]; } } } 归并排序性能分析时间复杂度
一趟归并,我们需要把遍历待排序序列遍历一遍,时间复杂度O(n)。
而归并排序的过程,需要把数组不断二分,这个时间复杂度是O(logn)。
所以归并排序的时间复杂度是O(nlogn)。
空间复杂度
使用了一个临时数组来存储合并的元素,空间复杂度O(n)。
稳定性
归并排序是一种稳定的排序方法。
算法名称 最好时间复杂度 最坏时间复杂度 平均时间复杂度 空间复杂度 是否稳定归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 稳定
快速排序 快速排序原理
快速排序是面试最高频的排序算法。
快速排序和上面的归并排序一样,都是基于分治思想的,大概过程:
选出一个基准数,基准值一般取序列最左边的元素
重新排序序列,比基准值小的放在基准值左边,比基准值大的放在基准值右边,这就是所谓的分区
快速排序动图如下:
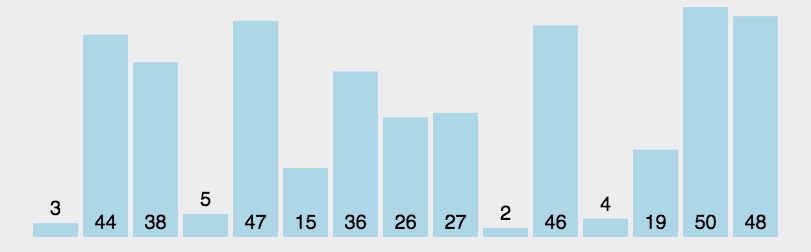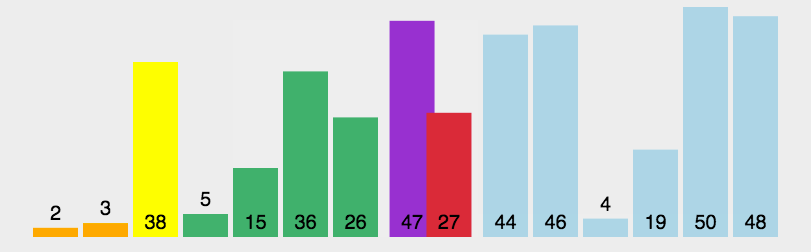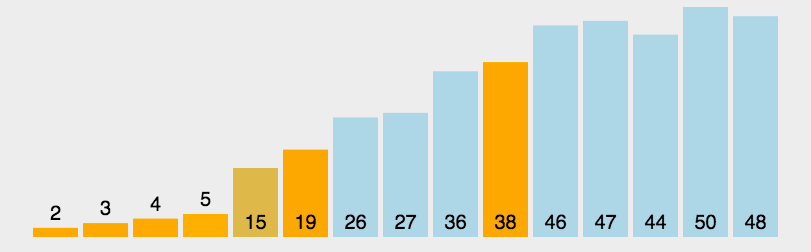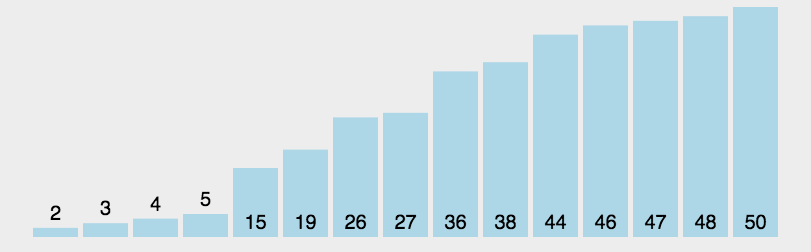
我们来看一个完整的快速排序图示: