万字长文|十大基本排序，一次搞定！ (4)

选择一个数作为基准数pivot，同时设定一个标记 mark 代表左边序列最右侧的下标位置，接下来遍历数组，如果元素大于基准值，无操作，继续遍历，如果元素小于基准值，则把 mark + 1 ，再将 mark 所在位置的元素和遍历到的元素交换位置，mark 这个位置存储的是比基准值小的数据，当遍历结束后，将基准值与 mark 所在元素交换位置。

public class QuickSort0 { public void sort(int[] nums) { quickSort(nums, 0, nums.length - 1); } public void quickSort(int[] nums, int left, int right) { //结束条件 if (left >= right) { return; } //分区 int partitonIndex = partion(nums, left, right); //递归左分区 quickSort(nums, left, partitonIndex - 1); //递归右分区 quickSort(nums, partitonIndex + 1, right); } //分区 public int partion(int[] nums, int left, int right) { //基准值 int pivot = nums[left]; //mark标记初始下标 int mark = left; for (int i = left + 1; i <= right; i++) { if (nums[i] < pivot) { //小于基准值，则mark+1，并交换位置 mark++; int temp = nums[mark]; nums[mark] = nums[i]; nums[i] = temp; } } //基准值与mark对应元素调换位置 nums[left] = nums[mark]; nums[mark] = pivot; return mark; } } 双边扫描快速排序

还有另外一种双边扫描的做法。

选择一个数作为基准值，然后从数组左右两边进行扫描，先从左往右找到一个大于基准值的元素，将它填入到right指针位置，然后转到从右往左扫描，找到一个小于基准值的元素，将他填入到left指针位置。

public class QuickSort1 { public int[] sort(int[] nums) { quickSort(nums, 0, nums.length - 1); return nums; } public void quickSort(int[] nums, int low, int high) { if (low < high) { int index = partition(nums, low, high); quickSort(nums, low, index - 1); quickSort(nums, index + 1, high); } } public int partition(int[] nums, int left, int right) { //基准值 int pivot = nums[left]; while (left < right) { //从右往左扫描 while (left < right && nums[right] >= pivot) { right--; } //找到第一个比pivot小的元素 if (left < right) nums[left] = nums[right]; //从左往右扫描 while (left < right && nums[left] <= pivot) { left++; } //找到第一个比pivot大的元素 if (left < right) nums[right] = nums[left]; } //基准数放到合适的位置 nums[left] = pivot; return left; } } 快速排序性能分析

时间复杂度

快速排序的时间复杂度和归并排序一样，都是O(nlogn)，但是这是最优的情况，也就是每次都能把数组切分到两个差不多大小的子数组。

如果出现极端情况，例如一个有序的序列[5,4,3,2,1] ，选基准值为5，那么需要切分n-1次才能完成整个快速排序的过程，这种情况时间复杂度就退化到了O(n²)。

空间复杂度

快速排序是一种原地排序的算法，空间复杂度是O(1)。

稳定性

快排的比较和交换是跳跃进行的，所以快排是一种不稳定的排序算法。

算法名称 最好时间复杂度 最坏时间复杂度 平均时间复杂度 空间复杂度 是否稳定
快速排序   O(nlogn)   O(n²)   O(nlogn)   O(1)   不稳定  
堆排序 堆排序原理

还记得我们前面的简单选择排序吗？堆排序是简单选择排序的一种升级版。

在学习堆排序之前，什么是堆呢？

完全二叉树是堆的一个比较经典的堆实现。

我们先来了解一下什么是完全二叉树。

简答说，如果节点不满，那它不满的部分只能在最后一层的右侧。

我们来看几个示例。

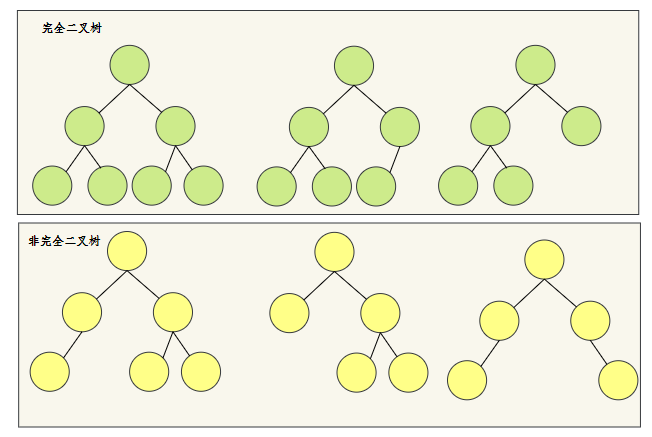
相信看了这几个示例，就清楚什么是完全二叉树，什么是非完全二叉树。

那堆又是什么呢？

必须是完全二叉树

任一节点的值必须是其子树的最大值或最小值

最大值时，称为“最大堆”，也称大顶堆；

最小值时，称为“最小堆”，也称小顶堆。

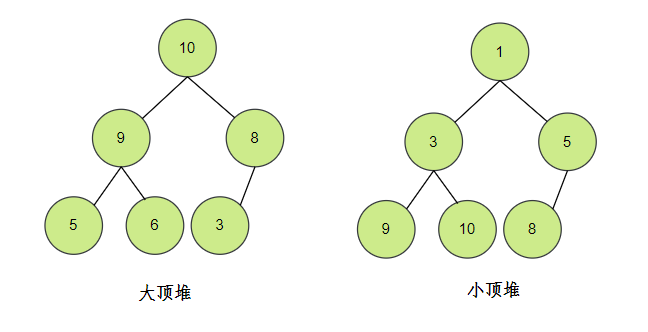
因为堆是完全二叉树，所以堆可以用数组存储。

按层来将元素存储到数组对应位置，从下标1开始存储，可以省略一些计算。

好了，我们现在对堆已经有一些了解了，我们来看一下堆排序是什么样的呢？[2]

建立一个大顶堆

将堆顶元素（最大值）插入数组末尾

让新的最大元素上浮到堆顶

重复过程，直到排序完成

动图如下（来源参考[1]）：

关于建堆，有两种方式，一种是上浮，一种是下沉。

上浮是什么呢？就是把子节点一层层上浮到合适的位置。

下沉是什么呢？就是把堆顶元素一层层下沉到合适的位置。