word emedding技术如word2vec,glove等已经广泛应用于NLP,极大地推动了NLP的发展。既然词可以embedding,句子也应该可以(其实,万物皆可embedding,Embedding is All You Need ^_^)。近年来(2014-2018),许多研究者在研究如何进行句子表示学习,从而获得质量较高的句子向量(sentence embedding)。事实上,sentence embedding在信息检索,句子匹配,句子分类等任务上均有广泛应用,并且上述任务往往作为下游任务来评测sentence embedding的好坏。本文将介绍如何用无监督学习方法来获取sentence embedding,是对近期阅读的sentence embedding论文笔记的总结。欢迎转载,请保留原文链接https://www.cnblogs.com/llhthinker/p/10335164.html
2. 基于词向量的词袋模型获取sentence embedding最直接最简单的思路就是对一个句子中所有词的word embedding进行组合。这种方法最明显的缺点是没有考虑词序信息,但是足够简单高效,在一些任务上是很好的baseline。
2.1 平均词向量与TFIDF加权平均词向量平均词向量就是将句子中所有词的word embedding相加取平均,得到的向量就当做最终的sentence embedding。这种方法的缺点是认为句子中的所有词对于表达句子含义同样重要。TFIDF加权平均词向量就是对每个词按照tfidf进行打分,然后进行加权平均,得到最终的句子表示。
2.2 SIF加权平均词向量发表于2016年的论文提出了一种非常简单但是具有一定竞争力的句子向量表示算法。算法包括两步,第一步是对句子中所有的词向量进行加权平均,得到平均向量\(v_s\);第二步是移出(减去)\(v_s\)在所有句子向量组成的矩阵的第一个主成分(principal component / singular vector)上的投影,因此该算法被简记为WR(W:weighting, R: removing)。
第一步主要是对TFIDF加权平均词向量表示句子的方法进行改进。论文提出了一种平滑倒词频 (smooth inverse frequency, SIF)方法用于计算每个词的加权系数,具体地,词\(w\)的权重为\(a / (a+p(w))\),其中\(a\)为平滑参数,\(p(w)\)为(估计的)词频。直观理解SIF,就是说频率越低的词在当前句子出现了,说明它在句子中的重要性更大,也就是加权系数更大。事实上,如果把一个句子认为是一篇文档并且假设该句中不出现重复的词(TF=1),那么TFIDF将演变成IF,即未平滑的倒词频。但是相较于TFIDF这种经验式公式,论文通过理论证明为SIF提供理论依据。对于第二步,个人的直观理解是移出所有句子的共有信息,因此保留下来的句子向量更能够表示本身并与其它句子向量产生差距。算法描述如下(其中\(v_s, u\)的shape均为[d, 1],\(uu^T\)为[d,d]的矩阵,d为词向量维度):

论文实验表明该方法具有不错的竞争力,在大部分数据集上都比平均词向量或者使用TFIDF加权平均的效果好,在使用PSL作为词向量时甚至能达到最优结果。当然,由于PSL本身是基于有监督任务(短语对)来训练词向量,因此PSL+WR能在文本蕴含或相似度计算任务上达到甚至打败LSTM的效果也在情理之中。代码开源在https://github.com/PrincetonML/SIF
3. 无监督句子表示学习下面介绍的方法是在无标签语料上训练句子表示学习模型,基本思想都是在无标签训练数据上设计监督学习任务进行学习,因此这里所说的无监督句子表示学习着重于训练数据是无标签的。
3.1 Paragraph Vector: PV-DM与PV-DBOW发表于2014年的论文Distributed representations of sentences and documents提出了两个模型用于学习句子和文档分布式表示(段落向量,Paragraph vector)。Paragraph Vector: A distributed memory model(PV-DM) 是论文提出的第一个学习段落向量的模型,如下图:
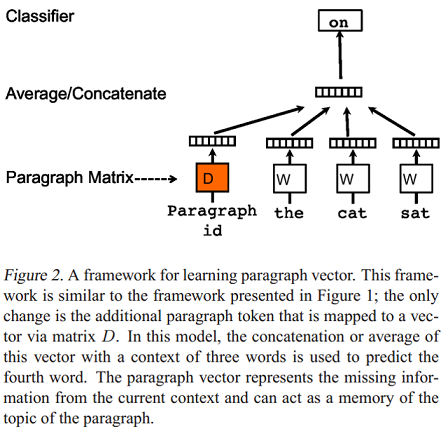
模型的具体步骤如下:
每个段落都映射到一个唯一的向量,由矩阵\(D\)中的一列表示,每个词也被映射到一个唯一的向量,表示为\(W\) ;
对当前段落向量和当前上下文所有词向量一起进行取平均值或连接操作,生成的向量用于输入到softmax层,以预测上下文中的下一个词: \[y=b+Uh(w_{t-k}, \dots, w_{t+k}; W; D)\]
这个段落向量可以被认为是另一个词。可以将它理解为一种记忆单元,记住当前上下文所缺失的内容或段落的主题 。矩阵\(D\) 和\(W\) 的区别是:

