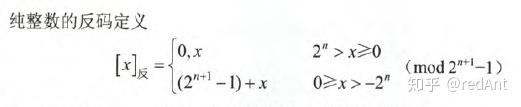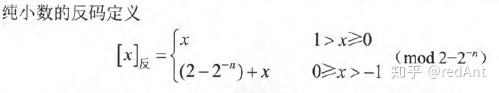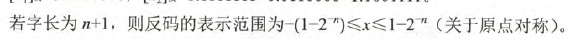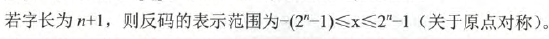对于纯小数:
对于纯整数:
所以,*记住上面的表示范围就够了*,我们具体看看运算过程,取反操作就是将原码中的0换成1,1换成0.就完事了。
当X = +1101时,X反 = 0,1101 当X = -1101时,
X反 = 1,0010(当为负数的时候,符号位不变,数值位执行取反操作)
当X = +0.0110时,X反 = 0.0110 当X = -0.0110时,X反 = 1.1001
对于0来说,反码的表示方式也有两种(0,000或者1,111),这就自己去写了。
0的反码表示不唯一
三种之间的关系:
三种机器码的最高位均为符号位,符号位与数值位用逗号隔开
当真值为正时,原码补码反码表示方式相同。
当真值为负时,三者表现都不同,但是符号位都用1表示,补码可以用“原码求反(不含符号位)后加1”求得。而反码是原码除了符号位以外的部分都进行取反操作。
其中0在移码和补码中的表示方式都是唯一的。
移码当真值用补码表示的时候,由于符号位与数值位一起编码,这与习惯上表示不同,我们很难从补码形式上直接判断真值的大小。但是如果对每个真值位(注意不包含符号位),都加上一个2^n(n为整数位),那么在数轴上,移码表示的范围恰好对应真值在数轴上移动2的n次方个单元。所以叫做移码。
它常常用来表示浮点数的阶数,因为它只能表示整数。 对于移码来说,0的表示是唯一的,假设字长为6位(含一个符号位)那么0的表示为:
+0移 = (2^5) + 0 =1,00000
-0移 = (2^5) - 0 =1,00000
特点:
1. 0 的表示方式唯一
2. 对于同一个真值,移码和补码相差一个符号位,且相反,例如:-11110 补码为1,00010,移码为:000010
3. 引入移码是为了直观的判断真值大小,所以移码大,真值就大
二、二进制与16进制
三、强制类型转换
基本数据类型整型(int):即定点整数,在寄存器中一般用补码表示,其最高位代表符号位,一般是4个字节。具体的位数跟变异平台有关。
无符号整数(unsigned):无符号,即不考虑数据位,二进制码表示的数就是其值。一般用补码表示。
长整型和短整型(long short):用补码表示,这只是位数不同罢了(一个长一个短)。
单精度浮点数和双精度浮点数(float double):就是我们平时说的小数点会移动的小数,前面的32位,后面的是64位。
数据间的保留,当计算记过超出机器所能表示的范围的时候,就会发生“溢出现象”。此时面临一个问题,那么是丢掉前面的N位还是丢掉后面的N位呢?一般我们选择保留后面的N位,丢掉前面的N位,若丢掉后发现不能表示正确的结果,说明产生溢出,还有一种情况就是不受影响了。
强制类型转换实际上是位值不变,只是改变了解释这些位的方式。
当数据太大,用二进制不好表示的时候我们选择用16进制(在之前提到过),分别是0x000286a1,0x86a1,0xffff7751, 0x7751,可以看出大字节转向小字节的转换的规则是:低位直接赋值(赋几位就看你的数据占几位,比如short占2字节,16位,一个16进制数代表4位2进制数),高位直接截断。