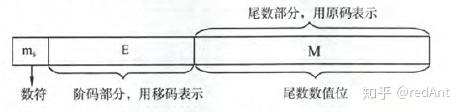
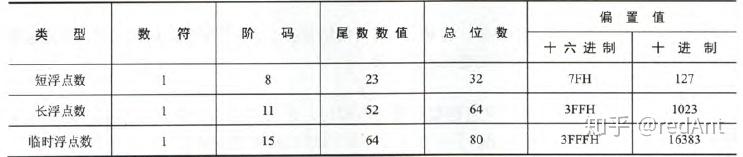
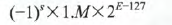根据浮点数的位数的不同,常见的浮点数有三种,短浮点数(float),长浮点数(double),临时浮点数。具体形式如下:
考试中,最常出现的当属短浮点数(float)了,因为长浮点数位数较多且原理与短浮点数一致。
1. 最高位为符号位,占用一位的空间
2. 阶码为8位,以移码的方式存储,阶码表示的范围为[1 ~ (2^8) - 1],为什么不是0-255?因为全0用来表示无穷大,全0表示非规格化数。
3. 尾数数值位为23位,在这里采用了隐藏位策略,由于我们规定了尾数最高位为1,也就是说数值位的第一位总会是1,所以我们可以采用23位来表示24位的数(我们把最高位的数值位隐藏了起来)。即不在23位数值位中存储这个1(这部分内容经常考!!)
4. 偏置值,对于float数而言,偏置值为127((2^7) - 1,其中,全一表示无穷大,至于为什么是7次方不是8次方,回顾移码的定义),表示阶码的移动。在存储浮点数阶码之前,要将偏置值加到阶码的真值上。比如阶码为3,那么移码表示的阶码为: 127 + 3 = 130(80H)。
所以,规格化后,float数的真值为:
其中 s = 0代表正数,s = 1 代表负数。由我们刚刚讨论出来的各个字段的范围可以得到float浮点数的表示范围: 显然,当E = 1,M= 0 的时候,浮点数最小, 当 E = 254, M = 111111...(23个1).的时候,浮点数最大;
浮点数的加减运算同定点数相同,浮点数的加减也采用补码的形式运算,不同的是,浮点数运算的过程较为麻烦。
1. 对阶 即小数点的位置对齐,此时两个浮点数的阶码相等。因此我们首先得得出两个浮点数相差几阶。由小阶转向大阶,具体操作是将数值部分右移一位, 此时阶码 +1。(这里面隐含着舍弃掉有效位的风险)
2. 尾数求和 对阶后就好办了,对阶完相当于小数点位置确定,直接进行定点数的加减。
3. 规格化 规格化,浮点数的规格化通常采用双符号位,前面我们已经说过双符号位这个概念了。
符号位和最高位相同时需要左规,溢出时需要右规 采用双符号位来计算
4. 舍入 在对阶和右规的过程中,尾数的低位有效位位很可能移丢(因为是小转大),这时候就会影响精度产生误差(注意,产生误差≠结果错误)。这样的溢出我们称为尾数溢出。因此必须对尾数进行舍入。常用的方法有:
恒置“1”法:无论右移舍去的是谁,都在末尾添加1
舍“0”入“1”法:右移过程中,尾数是0则舍去,是1,则尾数末尾加1.(存在尾数再次溢出的风险)