输出的数用16进制表示我就不说了,结论:从短字长到长字长的转换,相应的位值不变,向高位补充的数为符号位,所以-4321前面的16位都是1,因为它符号位是负号,如果是正号,那就变成0.
四、定点数及其加减运算
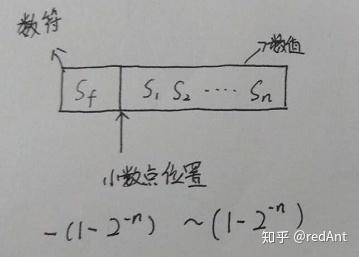
定点数定点数:小数点固定在某一个位置的数,有纯小数和纯整数之分。 假设数据用原码表示,那么: 纯小数可以表示为
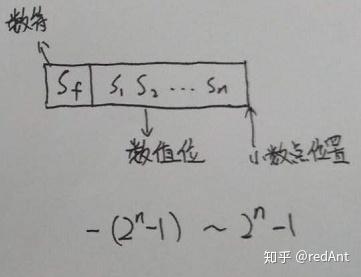
对于纯整数,可以表示为:
对比前面两幅图,只是小数点的位置不一样而已,在末尾表示整数,在内部表示小数。那么为什么表示整数的时候我们要减去一个1呢?我们回想一下原码的表示范围就会发现,原来是原码中0可以有两种不同的表示方式,因此减去一个重复的0.
定点数的运算定点数的运算主要包括,移位,加,减,乘,除运算。其中移位运算是基础,加减运算是重点,乘除运算过程繁杂,不大可能在考试中出现。
移位运算计算机中的定点数的小数点位置都是事先约定好的,所以二进制的小数点移动相当于乘上或者除以2的指数。就很像我们十进制中的移位:
15 -> 150 //小数点右移一位 相当于乘10
15 ->1.5 //小数点左移一位,相当于除10
那么类比到二进制来说,就是乘上或者除以2^n。 对于有符号数的移位,我们称为算术移位,移位运算也称移位操作。
操作的规则如下:
无论是正数还是负数,移位前后符号位不变
真值为正的时候,左右移动均添0
若真值为负,那么分下面三种情况: (1) 原码添0 (2) 补码左移添0,右移添1 (3) 反码添1
移位可能带来的问题:
1. 对于正数而言:左移的时候最高位可能丢1,即把1移出去了,造成溢出。反之,右移有可能把最低位的1移出去,影响数据的精度。
2. 对于负数而言:原码与上述情况一致,因为都是添0,而反码的左移添加的是1,右移也是如此,因此均会造成0的丢失影响精度。对于补码来说做移高位丢0,右移丢1,精度都不对。
加/减运算计算机中,加法减法的运算是最基本的运算,其中我们平时的计算中也可以知道的是,减法可以当做加法进行运算。比如: A - B = A +(-B); 由于我们前面说过,引入补码的原因就是为了方便计算,所以我们都采用补码来进行运算的。
基本公式(或者说理论基础): [A]补_+ [B] 补= [A + B]补 [A]补 - [B]补 = [A]补 + [-B]补
其中 [-B]补 称为求补后的减数,由[B]补,连同符号位在内,每位取反,末位加1所得。
下面看两道计算题: (1)已知X = +1001 ,Y = -0101,求【X+Y】补,以及X+Y。
这里,我们可以明显的看到,在使用补码的运算中,符号位参与了编码并且一起参与了运算。因为符号位只有一位所以舍弃最高的一位。
(2)已知某机器字长为8位(含一位符号位),令A = 15,B =24, 求【A+B】补 和(A-B)。
考虑这样一个问题,机器字长仍为8位,其中A = -93,B = 45.按照计算规则,我们有: