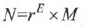很明显我们的计算过程是没有任何的问题的,但是问题出在我们把符号位参与了运算,我们根据常识知道结果为 -138 而138显然大于2^7 = 128.所以7位数值位不足以容纳超过128(不用减一因为补码表示的0唯一)的数。这种计算结果超过机器字长的现象我们称为溢出。
1. 肉眼观察法(做题好用) 这种往往看似很蠢的方式,却是最直观也是最有效的方法。就是通过对计算结果的大致估计来判断是否发生溢出。就比如上题,我们显然可以直接算出 -93-45 = -138,显然会发生溢出。对于一些判断溢出的方式往往这种方式最有效。
2. 一位符号位判断溢出(计算机中判断方式之一) 我们先看看溢出的必要条件是什么,同号相加,异号相减才有可能发生溢出。因此无论是做加法还是减法,只要实际参与操作的两个数(减法为【-B】补),符号相同,结果又与原操作数符号不同,即可以说明发生了溢出。
看下面一道例题: 设某机器字长为4位(含一位符号位) 当A = 5,B = 4时,有:
当A = -5,B = -4时,有:
这个时候产生了两个符号位,我们舍去最高的符号位,剩下0为符号位。
3. 两位符号位判断溢出 两位符号位的补码,也称变形补码。即在原符号位的前面加多一位符号位,这个加上去的符号跟之前的符号位一样。
比如: 【X】补 = -0.1011 加多一位符号位变为 11.1011
【X】补 = 0.1011 加多一位符号位变为 00.1011
原理:当结果的2位符号位不同时(即01或者10),表示溢出,且高位(就是第一位)的符号位永远代表着真正的符号。 举个例题:
五、浮点数及其加减运算
相对于定点数,浮点数就是小数点可以浮动的数。通常用来表示数值范围相差很大的数(比如太阳的质量跟电子的质量相差)。 通常我们使用这样的表达式来表示浮点数:
其中,r表示底(因为是指数的形式,一般取2的n次方),E表示阶码(阶码可正可负)。M为位数(可正可负)。 当r = 10的时候,就是我们熟悉的科学计数法。在计算机中我们研究的是r = 2的时候。
规格化数与浮点数的规格化为了提高数据的精确度以及便于比较浮点数的大小,在计算机中规定浮点数的尾数用纯小数表示。其中尾数最高位为1的浮点数称为规格化数。比如 N = 0.110101 X 2^10.尾数的最高位为1.所以称为规格化数。 为了提高浮点数的精确度,要求其尾数必须为规格化数,如果不是规格化数,那么就要修改阶码的值并同时左右移尾数的方法,使其变为规格化数。 根据尾数的移动位置,我们将规格化分为左规和右规(待会详细说)。我们先来看看一个十进制数的移动:
二进制的移动也是如此的。 因此我们得到这样的结论:
从图中我们可以看出至少这几点:
1. 对于原码而言,其规格化数的最高位一定是1
2. 对于补码而言,其规格化数的最高位一定与符号位相反
3. 对于正数,无论其是原码还是补码,规格化后的形式一样
4. 对于负数,补码的规格化数是原码规格化数的除了规格化位以外的全部取反
IEEE754标准现代计算机的浮点数一般采用IEEE定制的国际标准,这种标准形式如下: