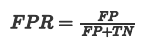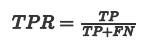x 轴为假阳性率(FPR):在所有的负样本中,分类器预测错误的比例
y 轴为真阳性率(TPR):在所有的正样本中,分类器预测正确的比例(等于Recall)
为了更好地理解ROC曲线,我们使用具体的实例来说明:
如在医学诊断的主要任务是尽量把生病的人群都找出来,也就是TPR越高越好。而尽量降低没病误诊为有病的人数,也就是FPR越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的TPR应该会很高,但是FPR也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么TPR达到1,FPR也为1。
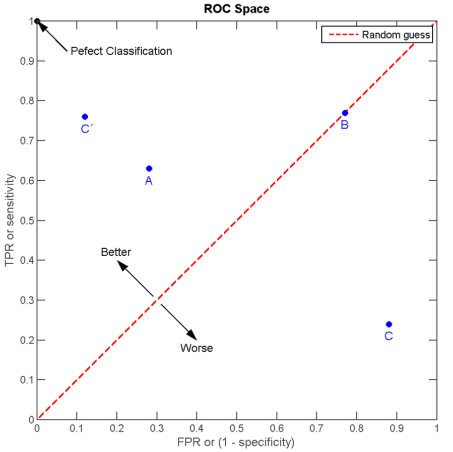
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间:
我们可以看出,左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对。点A(TPR>FPR),医生A的判断大体是正确的。中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到 ROC 曲线。
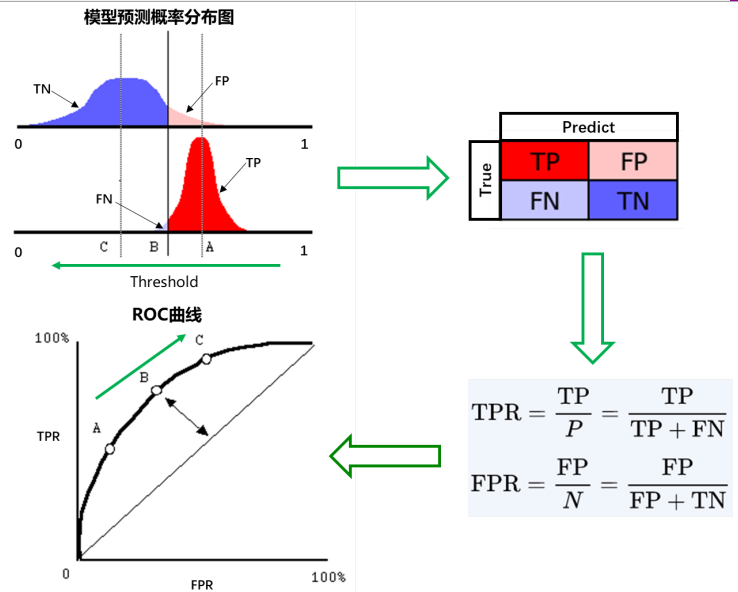
假设下图是某医生的诊断统计图,为未得病人群(上图)和得病人群(下图)的模型输出概率分布图(横坐标表示模型输出概率,纵坐标表示概率对应的人群的数量),显然未得病人群的概率值普遍低于得病人群的输出概率值(即正常人诊断出疾病的概率小于得病人群诊断出疾病的概率)。
竖线代表阈值。显然,图中给出了某个阈值对应的混淆矩阵,通过改变不同的阈值 ,得到一系列的混淆矩阵,进而得到一系列的TPR和FPR,绘制出ROC曲线。
阈值为1时,不管你什么症状,医生均未诊断出疾病(预测值都为N),此时 ,位于左下。阈值为 0 时,不管你什么症状,医生都诊断结果都是得病(预测值都为P),此时 ,位于右上。
2.6.2 AUC
AUC定义:
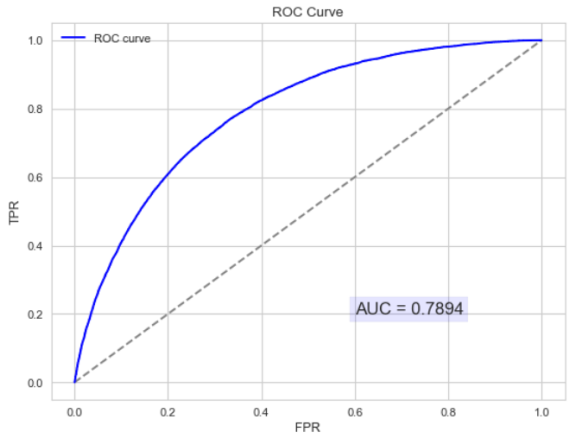
AUC 值为 ROC 曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器。
0.5 < AUC < 1,优于随机猜测。有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
注:对于AUC小于 0.5 的模型,我们可以考虑取反(模型预测为positive,那我们就取negtive),这样就可以保证模型的性能不可能比随机猜测差。
以下为ROC曲线和AUC值的实例:
AUC的物理意义 AUC的物理意义正样本的预测结果大于负样本的预测结果的概率。所以AUC反应的是分类器对样本的排序能力。另外值得注意的是,AUC对样本类别是否均衡并不敏感,这也是不均衡样本通常用AUC评价分类器性能的一个原因。
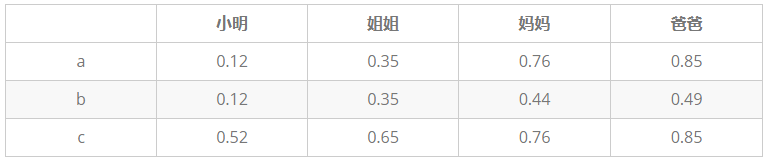
问题 13 :小明一家四口,小明5岁,姐姐10岁,爸爸35岁,妈妈33岁,建立一个逻辑回归分类器,来预测小明家人为成年人概率。
以下为三种模型的输出结果,求三种模型的 AUC :