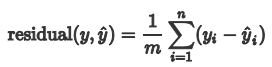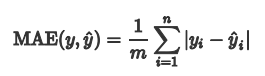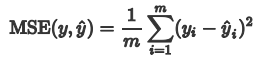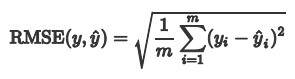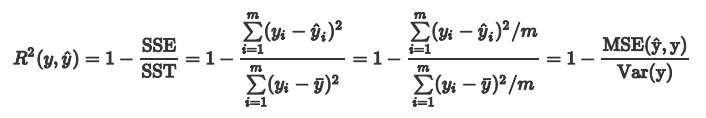参考:https://zhuanlan.zhihu.com/p/36305931 1、回归(Regression)算法指标
Mean Absolute Error 平均绝对误差
Mean Squared Error 均方误差
Root Mean Squared Error:均方根误差
Coefficient of determination 决定系数
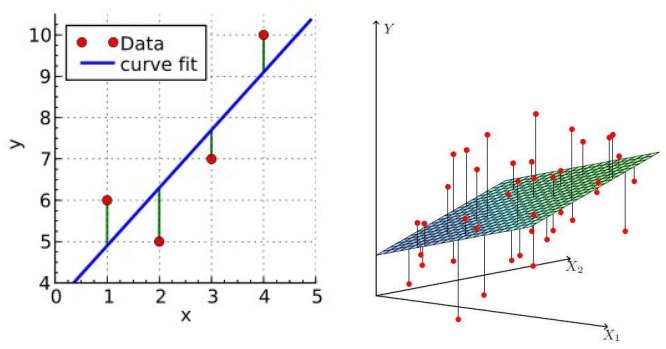
以下为一元变量和二元变量的线性回归示意图:
怎样来衡量回归模型的好坏呢? 我们第一眼自然而然会想到采用残差(实际值与预测值差值)的均值来衡量,即:
问题 1:用残差的均值合理吗?
当实际值分布在拟合曲线两侧时,对于不同样本而言 有正有负,相互抵消,因此我们想到采用预测值和真实值之间的距离来衡量。
1.1 平均绝对误差 MAE平均绝对误差MAE(Mean Absolute Error)又被称为 L1范数损失。
问题 2:MAE有哪些不足?
MAE虽能较好衡量回归模型的好坏,但是绝对值的存在导致函数不光滑,在某些点上不能求导,可以考虑将绝对值改为残差的平方,这就是均方误差。
1.2 均方误差 MSE均方误差MSE(Mean Squared Error)又被称为 L2范数损失 。
问题 3: 还有没有比MSE更合理一些的指标?
由于MSE与我们的目标变量的量纲不一致,为了保证量纲一致性,我们需要对MSE进行开方 。
1.3 均方根误差 RMSE问题 4: RMSE有没有不足的地方?有没有规范化(无量纲化的指标)?
上面的几种衡量标准的取值大小与具体的应用场景有关系,很难定义统一的规则来衡量模型的好坏。比如说利用机器学习算法预测上海的房价RMSE在2000元,我们是可以接受的,但是当四五线城市的房价RMSE为2000元,我们还可以接受吗?下面介绍的决定系数就是一个无量纲化的指标。
1.4 决定系数 R^2变量之所以有价值,就是因为变量是变化的。什么意思呢?比如说一组因变量为[0, 0, 0, 0, 0],显然该因变量的结果是一个常数0,我们也没有必要建模对该因变量进行预测。假如一组的因变量为[1, 3, 7, 10, 12],该因变量是变化的,也就是有变异,因此需要通过建立回归模型进行预测。这里的变异可以理解为一组数据的方差不为0。
决定系数又称为R^2 score,反映因变量的全部变异能通过回归关系被自变量解释的比例。
如果结果是0,就说明模型预测不能预测因变量。 如果结果是1。就说明是函数关系。 如果结果是0-1之间的数,就是我们模型的好坏程度。 化简上面的公式 ,分子就变成了我们的均方误差MSE,下面分母就变成了方差:
问题 5: 以上评估指标有没有缺陷,如果有,该怎样改进?
以上的评估指标是基于误差的均值对进行评估的,均值对异常点(outliers)较敏感,如果样本中有一些异常值出现,会对以上指标的值有较大影响,即均值是非鲁棒的。
1.5 解决评估指标鲁棒性问题我们通常用一下两种方法解决评估指标的鲁棒性问题:
剔除异常值